分析:以B1為坐標原點,建立空間坐標系,設正方體ABCD-A1B1C1D1的棱長為1,可求出各頂點的坐標
(1)分別求出AC與A1D方向向量,代入向量夾角公式,可得AC與A1D所成角的大小;
(2)要證明兩個平面平行,由面面平行的判定定理知:須在某一平面內尋找兩條相交且與另一平面平行的直線.求出AB1與C1D的方向向量,通過證明向量平行,得到AB1與C1D平行,同理證明出AD1與C1B平行,可得結論.
(3)求出A1C的方向向量,并證明A1C的方向向量是平面BDC1的法向量,可得A1C⊥平面BDC1.
解答:解:令正方體ABCD-A
1B
1C
1D
1的棱長為1,以B
1為坐標原點,建立空間坐標系如下圖所示:
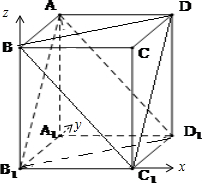
(1)則A(0,1,1),C(1,0,1),A
1(0,1,0),D(1,1,1)
∴
=(1,-1,0),
=(1,0,1)
設AC與A
1D所成角的大小為θ
則cosθ=
=
故θ=
證明:(2)∵
=
=(0,-1,-1)
∴AB
1∥C
1D,
又∵AB
1?平面AB
1D
1,C
1D?平面AB
1D
1,
∴C
1D∥平面AB
1D
1,
同理可證:C
1B∥平面AB
1D
1.
又C
1B∩C
1D=C
1,
∴平面AB
1D
1∥平面BDC
1.
(3)
=(1,-1,1),
=(1,1,0),
=(1,0,-1)
∴
•
=0,即
⊥
,即A
1C⊥BD
且
•
=0,即
⊥
,即A
1C⊥BC
1.
∵BD∩BC
1=B,BD,BC
1?平面BDC
1.
∴A
1C⊥平面BDC
1.
點評:第一問在使用傳統方法證明時,必須強調一作二證三計算的步驟,第二問在證明線面平行時,一定要強調平面外和平面內的直線.

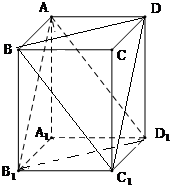 如圖,在正方體ABCD-A1B1C1D1中,求證:
如圖,在正方體ABCD-A1B1C1D1中,求證:


 導學全程練創優訓練系列答案
導學全程練創優訓練系列答案 若Rt△ABC中兩直角邊為a、b,斜邊c上的高為h,則
若Rt△ABC中兩直角邊為a、b,斜邊c上的高為h,則 若Rt△ABC中兩直角邊為a、b,斜邊c上的高為h,則
若Rt△ABC中兩直角邊為a、b,斜邊c上的高為h,則 如圖,在正方體ABCD-A1B1C1D1中,點P是上底面A1B1C1D1內一動點,則三棱錐P-ABC的主視圖與左視圖的面積的比值為( )
如圖,在正方體ABCD-A1B1C1D1中,點P是上底面A1B1C1D1內一動點,則三棱錐P-ABC的主視圖與左視圖的面積的比值為( )