
分析 (Ⅰ)求出函數的導數,通過函數的極值點,即可求a的值;
(Ⅱ)利用第一問,通過函數的極值點,判斷函數的單調性,求解函數的極值與端點值,即可得到結果.
解答 解:(Ⅰ)f'(x)=x2-ax-3,….(1分)
因為f(x)在x=-1處取得極值,所以f'(-1)=(-1)2+a-3=0,….(4分)
解得a=2,
經檢驗,a=2符合題意,因此a=2.….(6分)
(Ⅱ)由(Ⅰ)得$f(x)=\frac{1}{3}{x^3}-{x^2}-3x$,f'(x)=x2-2x-3=(x+1)(x-3),
令f'(x)=0,解得x1=-1,x2=3….(8分)
當x變化時,f'(x)、f(x)的變化情況如表
| x | 0 | (0,3) | 3 | (3,5) | 5 |
| f′(x) | 0 | - | 0 | + | 0 |
| f(x) | 0 | ↘ | -9 | ↗ | $\frac{5}{3}$ |
點評 本題考查函數的導數的應用,函數的極值以及函數的單調性函數的最值的求法,考查計算能力.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:填空題
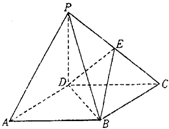 如圖,四棱錐P-ABCD的底面ABCD是正方形,側棱PD⊥底面ABCD,PD=DC,E是PC的中點.則二面角B-DE-C的平面角的余弦值是$\frac{\sqrt{3}}{3}$.
如圖,四棱錐P-ABCD的底面ABCD是正方形,側棱PD⊥底面ABCD,PD=DC,E是PC的中點.則二面角B-DE-C的平面角的余弦值是$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(6,6\sqrt{2})$或$(6,-6\sqrt{2})$ | B. | $(4,4\sqrt{3})$或$(4,-4\sqrt{3})$ | C. | (3,6)或(3,-6) | D. | $(9,6\sqrt{3})$或$(9,-6\sqrt{3})$ |
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com