
求證:(1)如果|α|<2,|β|<2,那么2|a|<4+b且|b|<4;
(2)如果2|a|<4+b且|b|<4,那么|α|<2,|β|<2.
思路解析:結合二次方程根的分布及絕對值的意義來求解.
證法一:設二次方程有兩個實數α,β,則判別式Δ=a2-4b≥0.
不妨取α=![]() (-a-
(-a-![]() ),β=
),β=![]() (-a+
(-a+![]() ).
).
(1)∵|α|<2,|β|<2,∴|b|=|αβ|=|α|·|β|<4,
且-2<![]() (-a-
(-a-![]() ),
),![]() (-a+
(-a+![]() )<2,即0≤
)<2,即0≤![]() <4-a,0<
<4-a,0<![]() ≤4+a.
≤4+a.
平方得a2-4b<16-8a+a2,a2-4b<16+8a+a2,
由此得-4(4+b)<8a<4(a+b),∴2|a|<4+b.
(2)由2|a|<4+b,得4+2a+b>0,即22+2a+b>0![]() f(2)>0,①
f(2)>0,①
即4-2a+b>0,即(-2)2+(-2)a+b>0![]() f(-2)>0.②
f(-2)>0.②
由此可知f(x)=0的每個實根或者在區間(-2,2)之內或者在(-2,2)之外,若兩根α、β均落在(-2,2)之外,則與|b|=|αβ|<4矛盾.
若α(或β)落在(-2,2)外,則由于|b|=|αβ|<4,另一個根β(或α)必須落在(-2,2)內,則與①、②式矛盾.
故|α|<2,|β|<2.
證法二:(1)由|α|<2,|β|<2,得α、β∈(-2,2).
令f(x)=x2+ax+b,則

![]()
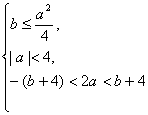
![]()
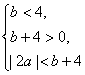
![]() 2|a|<b+4且|b|<4.
2|a|<b+4且|b|<4.
(2)條件可概括為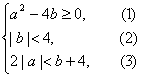
由(2)(3),得|a|<4![]() -2<-
-2<-![]() <2, (4)
<2, (4)
由(3),得-(b+4)<2a<b+4,
令f(x)=x2+ax+b,則f(-2)=4-2a+b>0,f(2)=4+2a+b>0,
∴α、β∈(-2,2),故|α|<2且|β|<2.
深化升華
把絕對值的意義,轉化為根的分布是解題的關鍵,結合函數在區間端點的值進行比較.


科目:高中數學 來源: 題型:
| b | i |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇省常州高級中學高三(上)期中數學試卷(理科)(解析版) 題型:填空題
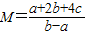 的最小值是 .
的最小值是 .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com