
【題目】某超市在元旦期間開展優惠酬賓活動,凡購物滿100元可抽獎一次,滿200元可抽獎兩次…依此類推.抽獎箱中有7個白球和3個紅球,其中3個紅球上分別標有10元,10元,20元字樣.每次抽獎要從抽獎箱中有放回地任摸一個球,若摸到紅球,根據球上標注金額獎勵現金;若摸到白球,沒有任何獎勵.
(Ⅰ)一次抽獎中,已知摸中了紅球,求獲得20元獎勵的概率;
(Ⅱ)小明有兩次抽獎機會,用![]() 表示他兩次抽獎獲得的現金總額,寫出
表示他兩次抽獎獲得的現金總額,寫出![]() 的分布列與數學期望.
的分布列與數學期望.
 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的長軸長是短軸長的
的長軸長是短軸長的![]() 倍,且過點
倍,且過點![]() .
.
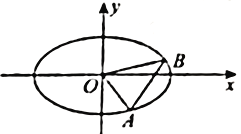
(1)求橢圓的標準方程;
(2)若![]() 的頂點
的頂點![]() 、
、![]() 在橢圓上,
在橢圓上, ![]() 所在的直線斜率為
所在的直線斜率為![]() ,
, ![]() 所在的直線斜率為
所在的直線斜率為![]() ,若
,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓過定點![]() ,且在
,且在![]() 軸上截得線段
軸上截得線段![]() 的長為 4,直線
的長為 4,直線![]() 交
交![]() 軸于點
軸于點![]() .
.
(1)求動圓圓心的軌跡![]() 的方程;
的方程;
(2)直線![]() 與軌跡
與軌跡![]() 交于
交于![]() 兩點,分別以
兩點,分別以![]() 為切點作軌跡
為切點作軌跡![]() 的切線交于點
的切線交于點![]() ,若
,若![]() .試判斷實數
.試判斷實數![]() 所滿足的條件,并說明理由.
所滿足的條件,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩焦點與短軸的一個端點的連線構成等腰直角三角形,
的兩焦點與短軸的一個端點的連線構成等腰直角三角形,
直線![]() 與以橢圓C的右焦點為圓心,以橢圓的長半軸長為半徑的圓相切.
與以橢圓C的右焦點為圓心,以橢圓的長半軸長為半徑的圓相切.
(Ⅰ)求橢圓C的方程;
(Ⅱ)設P為橢圓C上一點,若過點![]() 的直線
的直線![]() 與橢圓C相交于不同的兩點S和T,
與橢圓C相交于不同的兩點S和T,
滿足![]() (O為坐標原點),求實數
(O為坐標原點),求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市100戶居民的月平均用電量(單位:度),以![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() 分組的頻率分布直方圖如圖示.
分組的頻率分布直方圖如圖示.

(Ⅰ)求直方圖中![]() 的值;
的值;
(Ⅱ)求月平均用電量的眾數和中位數;
(Ⅲ)在月平均用電量為![]() ,
,![]() ,
,![]() 的三組用戶中,用分層抽樣的方法抽取10戶居民,則月平均用電量在
的三組用戶中,用分層抽樣的方法抽取10戶居民,則月平均用電量在![]() 的用戶中應抽取多少戶?
的用戶中應抽取多少戶?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com