
【題目】設點![]() 是拋物線
是拋物線![]() 上異于原點
上異于原點![]() 的一點,過點
的一點,過點![]() 作斜率為
作斜率為![]() 、
、![]() 的兩條直線分別交
的兩條直線分別交![]() 于
于![]() 、
、![]() 兩點(
兩點(![]() 、
、![]() 、
、![]() 三點互不相同).
三點互不相同).
(1)已知點![]() ,求
,求![]() 的最小值;
的最小值;
(2)若![]() ,直線
,直線![]() 的斜率是
的斜率是![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,當
,當![]() 時,
時,![]() 點的縱坐標的取值范圍.
點的縱坐標的取值范圍.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 或
或![]()
【解析】
(1)因為![]() ,設
,設![]() ,則
,則![]() ,由兩點間距離公式可求得:
,由兩點間距離公式可求得: ,即可得出
,即可得出![]() 的最小值;
的最小值;
(2)因為![]() ,所以
,所以![]() ,設
,設![]() 的直線方程
的直線方程![]() :
:![]() ,將
,將![]() 與
與![]() 聯立方程組,消掉
聯立方程組,消掉![]() ,通過韋達定理,將點
,通過韋達定理,將點![]() 坐標用
坐標用![]() 表示同理可得到
表示同理可得到![]() 坐標.即可求得直線
坐標.即可求得直線![]() 的斜率是
的斜率是![]() ,進而求得答案;
,進而求得答案;
(3)因為![]() ,故
,故![]() .
.![]() 、
、![]() 兩點拋物線上,可得
兩點拋物線上,可得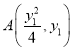 ,
, 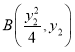 ,即可求得向量
,即可求得向量![]() 和
和![]() .由
.由![]() ,可得到關于
,可得到關于![]() 和
和![]() 方程,將方程可以看作關于
方程,將方程可以看作關于![]() 的一元二次方程, 因為
的一元二次方程, 因為![]() 且
且![]() ,
,![]() ,故此方程有實根,
,故此方程有實根,![]() ,即可求得
,即可求得![]() 點的縱坐標的取值范圍.
點的縱坐標的取值范圍.
(1)![]()
![]() 在
在![]() ,設
,設![]() ,則
,則![]()
由兩點間距離公式可求得:
令![]() ,
,![]()
![]()
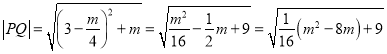
![]() (當
(當![]() 即
即![]() 取等號)
取等號)
![]()
![]() 的最小值
的最小值![]() .
.
(2)![]()
![]() ,
,![]() ,故
,故![]()
則![]() 的直線方程
的直線方程![]() :
: ![]()
將![]() 與
與![]() 聯立方程組,消掉
聯立方程組,消掉![]()
則:![]() ,得:
,得:
化簡為:![]() .
.
由韋達定理可得: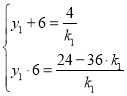 解得:
解得:![]()
![]() ,可得:
,可得: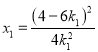 ,故
,故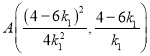
同理可得: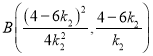
![]() 直線的斜率是
直線的斜率是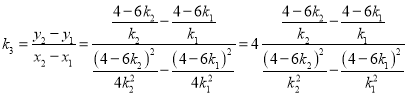
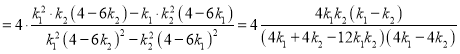
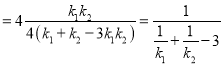
故:![]() 即
即![]()
![]() 的值為
的值為![]() .
.
(3)![]()
![]() ,
,![]() ,故
,故![]()
![]()
![]() ,
,![]() 在
在![]() 、
、![]() 兩點拋物線上
兩點拋物線上
![]()
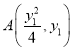 ,
, 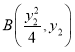
![]()
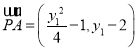 ,
,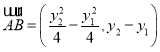
![]()
![]() ,故
,故 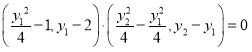
整理可得: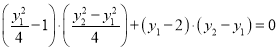
![]()
![]()
![]() 、
、![]() 、
、![]() 三點互不相同,故:
三點互不相同,故:![]() ,
,![]()
可得:![]() 即:
即:![]()
![]()
![]() 此方程可以看作關于
此方程可以看作關于![]() 的一元二次方程,
的一元二次方程,
![]()
![]() 且
且![]() ,
,![]() ,故此方程有兩個不相等的實根:
,故此方程有兩個不相等的實根:
![]() 即
即![]()
![]()
![]() 故:
故:![]()
解得: ![]() 或
或![]()
![]()
![]() 點的縱坐標的取值范圍:
點的縱坐標的取值范圍: ![]() 或
或![]() .
.


 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC-A1B1C1中,AB=AA1=![]() ,AC=2,∠BAC=∠A1AC=45°,∠BAA1=60°,F為棱AC的中點,E在棱BC上,且BE=2EC.
,AC=2,∠BAC=∠A1AC=45°,∠BAA1=60°,F為棱AC的中點,E在棱BC上,且BE=2EC.
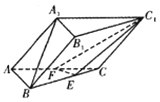
(Ⅰ)求證:A1B∥平面EFC1;
(Ⅱ)求三棱柱ABC-A1B1C1的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知空間中不同直線m、n和不同平面α、β,下面四個結論:
①若m、n互為異面直線,m∥α,n∥α,m∥β,n∥β,則α∥β;
②若m⊥n,m⊥α,n∥β,則α⊥β;
③若n⊥α,m∥α,則n⊥m;
④若α⊥β,m⊥α,n∥m,則n∥β.
其中正確的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在平面直角坐標系xOy中,已知橢圓C1:![]() ,橢圓C2:
,橢圓C2:![]() ,C2與C1的長軸長之比為
,C2與C1的長軸長之比為![]() ∶1,離心率相同.
∶1,離心率相同.
(1)求橢圓C2的標準方程;
(2)設點![]() 為橢圓C2上一點.
為橢圓C2上一點.
① 射線![]() 與橢圓C1依次交于點
與橢圓C1依次交于點![]() ,求證:
,求證:![]() 為定值;
為定值;
② 過點![]() 作兩條斜率分別為
作兩條斜率分別為![]() 的直線
的直線![]() ,且直線
,且直線![]() 與橢圓C1均有且只有一個公共點,求證:
與橢圓C1均有且只有一個公共點,求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}前n項和為Sn,滿足Sn+1=4an+2(n∈N+),且a1=1,
(1)若cn![]() ,求證:數列{cn}是等差數列.
,求證:數列{cn}是等差數列.
(2)求數列{an}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠今年初用128萬元購進一臺新的設備,并立即投入使用,計劃第一年維修、保養費用8萬元,從第二年開始,每年的維修、保養修費用比上一年增加4萬元,該設備使用后,每年的總收入為54萬元,設使用x年后設備的盈利總額y萬元.
(1)寫出y與x之間的函數關系式;
(2)從第幾年開始,該設備開始盈利?
(3)使用若干年后,對設備的處理有兩種方案:①年平均盈利額達到最大值時,以42萬元價格賣掉該設備;②盈利額達到最大值時,以10萬元價格賣掉該設備.問哪種方案處理較為合理?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的四個頂點組成的四邊形的面積為
的四個頂點組成的四邊形的面積為![]() ,且經過點
,且經過點 .
.

(1)求橢圓![]() 的方程;
的方程;
(2)若橢圓![]() 的下頂點為
的下頂點為![]() ,如圖所示,點
,如圖所示,點![]() 為直線
為直線![]() 上的一個動點,過橢圓
上的一個動點,過橢圓![]() 的右焦點
的右焦點![]() 的直線
的直線![]() 垂直于
垂直于![]() ,且與
,且與![]() 交于
交于![]() 兩點,與
兩點,與![]() 交于點
交于點![]() ,四邊形
,四邊形![]() 和
和![]() 的面積分別為
的面積分別為![]() .求
.求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com