
已知函數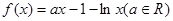
①當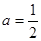 時,求函數在
時,求函數在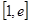 上的最大值和最小值;
上的最大值和最小值;
②討論函數的單調性;
③若函數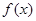 在
在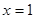 處取得極值,不等式
處取得極值,不等式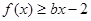 對
對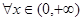 恒成立,求實數
恒成立,求實數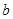 的取值范圍。
的取值范圍。
(1)最大值是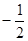 ,最小值是
,最小值是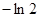 。(2)當
。(2)當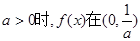 單調遞減,在
單調遞減,在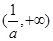 單調遞增,當
單調遞增,當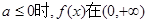 單調遞減(3)
單調遞減(3)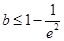
【解析】
試題分析:(1)當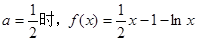
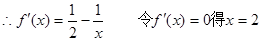 1分
1分
當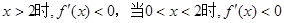
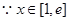
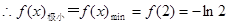 2分
2分
又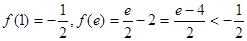

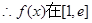 上的最大值是
上的最大值是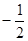 ,最小值是
,最小值是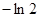 。
3分
。
3分
(2)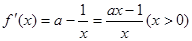
當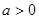 時,令
時,令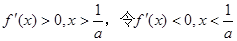 。
。
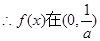 單調遞減,在
單調遞減,在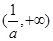 單調遞增
5分
單調遞增
5分
當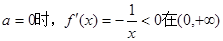 恒成立
恒成立
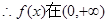 為減函數
6分
為減函數
6分
當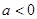 時,
時,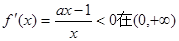 恒成立
恒成立
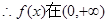 單調遞減 。
7分
單調遞減 。
7分
綜上,當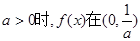 單調遞減,在
單調遞減,在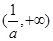 單調遞增,當
單調遞增,當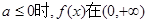 單調遞減
8分
單調遞減
8分
(3)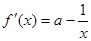 ,依題意:
,依題意: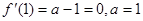
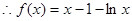 9分
9分
又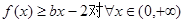 恒成立。即
恒成立。即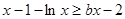
法(一)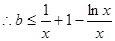 在
在 上恒成立
10分
上恒成立
10分
令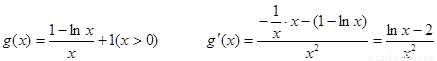 12分
12分
當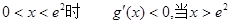 時
時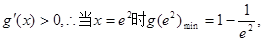
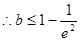 14分
14分
法(二)由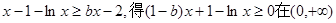 上恒成立。
上恒成立。
設 10分
10分
∴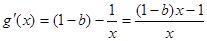 11分
11分
當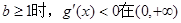 恒成立,無最值
恒成立,無最值
當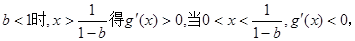
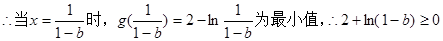
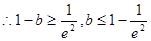 14分
14分
考點:本題考查了導數的運用
點評:對于函數與導數這一綜合問題的命制,一般以有理函數與半超越(指數、對數)函數的組合復合且含有參量的函數為背景載體,解題時要注意對數式對函數定義域的隱蔽,這類問題重點考查函數單調性、導數運算、不等式方程的求解等基本知識,注重數學思想的運用


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:高中數學 來源:2011屆山西大學附中高三第二學期高三第一次模擬測試數學試卷 題型:解答題
(12 分)
已知函數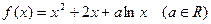 .
.
①當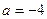 時,求
時,求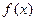 的最小值;
的最小值;
②若函數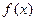 在區間
在區間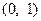 上為單調函數,求實數
上為單調函數,求實數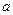 的取值范圍;
的取值范圍;
③當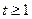 時,不等式
時,不等式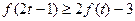 恒成立,求實數
恒成立,求實數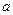 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年河北省館陶一中高二下學期期中考試文科數學試卷(帶解析) 題型:解答題
已知函數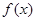 =
= .
.
(Ⅰ)當 時,求不等式
時,求不等式 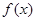 ≥3的解集;
≥3的解集;
(Ⅱ) 若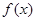 ≤
≤ 的解集包含
的解集包含 ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2014屆河北省高二下學期期中考試文科數學試卷(解析版) 題型:解答題
已知函數 =
= .
.
(Ⅰ)當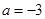 時,求不等式
時,求不等式  ≥3的解集;
≥3的解集;
(Ⅱ) 若 ≤
≤ 的解集包含
的解集包含 ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年江西省協作體高三第二次聯考數學理卷 題型:解答題
(本小題14 分)
已知函數 .
.
①當 時,求
時,求 的最小值;
的最小值;
②若函數 在區間
在區間 上為單調函數,求實數
上為單調函數,求實數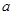 的取值范圍;
的取值范圍;
③當 時,不等式
時,不等式 恒成立,求實數
恒成立,求實數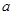 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com