
已知定義在區間 上的函數y=f(x)的圖象關于直線x=-
上的函數y=f(x)的圖象關于直線x=- 對稱,當x∈
對稱,當x∈ 時,函數f(x)=Asin(ωx+φ)
時,函數f(x)=Asin(ωx+φ) 的圖象如圖所示.
的圖象如圖所示.
(1)求函數y=f(x)在 上的表達式;
上的表達式;
(2)求方程f(x)= 的解.
的解.
(1)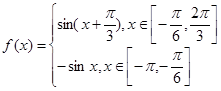 ;(2)∴x=-
;(2)∴x=-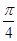 或-
或-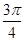 或-
或- 或
或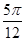 .
.
解析試題分析:(1)根據圖象中函數值的最大值判斷出A的值,利用函數圖象與x軸的交點判斷出函數的周期,進而求得ω,把點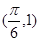 代入求得φ的值,則當
代入求得φ的值,則當 時,函數的解析式可得;進而利用函數圖象關于直線
時,函數的解析式可得;進而利用函數圖象關于直線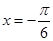 對稱利用
對稱利用 求得
求得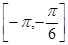 的函數解析式,最后綜合答案可得;(2)分別看
的函數解析式,最后綜合答案可得;(2)分別看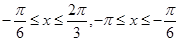 ,利用(1)中的函數解析式,求得x的值.
,利用(1)中的函數解析式,求得x的值.
試題解析:(1)當x∈ 時,A=1,
時,A=1,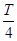 =
= -
- ,T=2π,ω=1.且f(x)=sin(x+φ)過點
,T=2π,ω=1.且f(x)=sin(x+φ)過點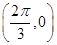 ,則
,則 +φ=π,φ=
+φ=π,φ= .f(x)=sin
.f(x)=sin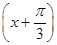 .當-π≤x<-
.當-π≤x<- 時,-
時,- ≤-x-
≤-x- ≤
≤ ,
,
f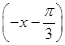 =sin
=sin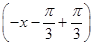 ,而函數y=f(x)的圖象關于直線x=-
,而函數y=f(x)的圖象關于直線x=- 對稱,則f(x)=f
對稱,則f(x)=f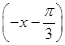 ,
,
即f(x)=sin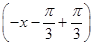 =-sinx,-π≤x<-
=-sinx,-π≤x<- .∴
.∴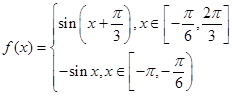
(2)當- ≤x≤
≤x≤ 時,
時, ≤x+
≤x+ ≤π,由f(x)=sin
≤π,由f(x)=sin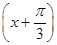 =
= ,得x+
,得x+ =
=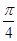 或
或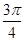 ,x=-
,x=- 或
或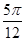 .當-π≤x<-
.當-π≤x<- 時,由f(x)=-sinx=
時,由f(x)=-sinx= ,sinx=-
,sinx=- ,得x=-
,得x=-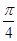 或-
或-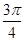 .∴x=-
.∴x=-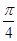 或-
或-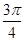 或-
或- 或
或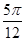 .
.
考點:三角函數的圖像與解析式


 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:解答題
已知向量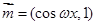 ,
,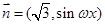 (
(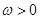 ),函數
),函數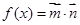 ,且
,且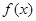 圖象上一個最高點為
圖象上一個最高點為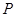
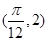 ,與
,與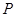 最近的一個最低點的坐標為
最近的一個最低點的坐標為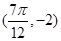 .
.
(1)求函數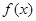 的解析式;
的解析式;
(2)設 為常數,判斷方程
為常數,判斷方程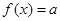 在區間
在區間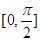 上的解的個數;
上的解的個數;
(3)在銳角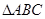 中,若
中,若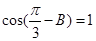 ,求
,求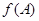 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com