
【題目】已知函數![]()
(I)若函數![]() 的圖象在
的圖象在![]() 處的切線斜率為1,求實數
處的切線斜率為1,求實數![]() 的值;
的值;
(Ⅱ)求函數![]() 的單調區間;
的單調區間;
(Ⅲ)若函數![]() 在[1,2]上是減函數,求實數
在[1,2]上是減函數,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;
;
(2)![]() 的單調遞減區間是
的單調遞減區間是![]() ;單調遞增區間是
;單調遞增區間是![]() ;
;
(3)![]()
【解析】
第一問中![]() , 由已知
, 由已知![]() ,解得
,解得![]()
第二問中,因為函數![]() 的定義域為
的定義域為![]() .
.![]()
可知函數![]() 的單調遞減區間是
的單調遞減區間是![]() ;單調遞增區間是
;單調遞增區間是![]()
第三問由![]() 得
得![]()
由已知函數![]() 為
為![]() 上的單調減函數,
上的單調減函數,
則![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立.
上恒成立.
即![]() 在
在![]() 上恒成立.分離參數法得到。
上恒成立.分離參數法得到。
解:(1)![]() ……………………………………………1分
……………………………………………1分
由已知![]() ,解得
,解得![]() . …………………………………………………3分
. …………………………………………………3分
(2)函數![]() 的定義域為
的定義域為![]() .
.![]() .
.
當![]() 變化時,
變化時,![]() 的變化情況如下:
的變化情況如下:
|
|
|
|
| - |
| + |
|
| 極小值 |
|
由上表可知,函數![]() 的單調遞減區間是
的單調遞減區間是![]() ;單調遞增區間是
;單調遞增區間是![]() . ……6分
. ……6分
(3)由![]() 得
得![]() , ………………………………8分
, ………………………………8分
由已知函數![]() 為
為![]() 上的單調減函數,
上的單調減函數,
則![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立.
上恒成立.
即![]() 在
在![]() 上恒成立. ………………………………………………………10分
上恒成立. ………………………………………………………10分
令![]() ,在
,在![]() 上
上![]() ,
,
所以![]() 在
在![]() 為減函數.
為減函數.![]() ,所以
,所以![]() . ……………………12分
. ……………………12分


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源: 題型:
【題目】以平面直角坐標系的原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,已知直線
軸的正半軸為極軸,建立極坐標系,已知直線![]() 的參數方程是
的參數方程是 (m>0,t為參數),曲線
(m>0,t為參數),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與曲線
,與曲線![]() 交于點
交于點![]() ,且
,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究學生的數學核心素養與抽象能力(指標![]() )、推理能力(指標
)、推理能力(指標![]() )、建模能力(指標
)、建模能力(指標![]() )的相關性,將它們各自量化為1、2、3三個等級,再用綜合指標
)的相關性,將它們各自量化為1、2、3三個等級,再用綜合指標![]() 的值評定學生的數學核心素養,若
的值評定學生的數學核心素養,若![]() ,則數學核心素養為一級;若
,則數學核心素養為一級;若![]() ,則數學核心素養為二級;若
,則數學核心素養為二級;若![]() ,則數學核心素養為三級,為了了解某校學生的數學核心素養,調查人員隨機訪問了某校10名學生,得到如下數據:
,則數學核心素養為三級,為了了解某校學生的數學核心素養,調查人員隨機訪問了某校10名學生,得到如下數據:
學生編號 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)在這10名學生中任取兩人,求這兩人的建模能力指標相同條件下綜合指標值也相同的概率;
(2)在這10名學生中任取三人,其中數學核心素養等級是一級的學生人數記為![]() ,求隨機變量
,求隨機變量![]() 的分布列及其數學期望.
的分布列及其數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 設命題p:函數y=![]() 在定義域上為減函數;命題q:a,b∈(0,+∞),當a+b=1時,
在定義域上為減函數;命題q:a,b∈(0,+∞),當a+b=1時,![]() +
+![]() =3.以下說法正確的是( )
=3.以下說法正確的是( )
A. p∨q為真B. p∧q為真
C. p真q假D. p,q均假
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某次的一次學科測試成績的莖葉圖和頻率分布直方圖都受到不同程度的污損,可見部分如圖.

(Ⅰ)求參加測試的總人數及分數在[80,90)之間的人數;
(Ⅱ)若要從分數在[80,100)之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,恰有一份分數在[90,100)之間的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高一年級共有![]() 名學生,其中男生
名學生,其中男生![]() 名,女生
名,女生![]() 名,該校組織了一次口語模擬考試(滿分為
名,該校組織了一次口語模擬考試(滿分為![]() 分).為研究這次口語考試成績為高分是否與性別有關,現按性別采用分層抽樣抽取
分).為研究這次口語考試成績為高分是否與性別有關,現按性別采用分層抽樣抽取![]() 名學生的成績,按從低到高分成
名學生的成績,按從低到高分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七組,并繪制成如圖所示的頻率分布直方圖.已知
七組,并繪制成如圖所示的頻率分布直方圖.已知![]() 的頻率等于
的頻率等于![]() 的頻率,
的頻率,![]() 的頻率與
的頻率與![]() 的頻率之比為
的頻率之比為![]() ,成績高于
,成績高于![]() 分的為“高分”.
分的為“高分”.

(1)估計該校高一年級學生在口語考試中,成績為“高分”的人數;
(2)請你根據已知條件將下列![]() 列聯表補充完整,并判斷是否有
列聯表補充完整,并判斷是否有![]() 的把握認為“該校高一年級學生在本次口語考試中成績及格(
的把握認為“該校高一年級學生在本次口語考試中成績及格(![]() 分以上(含
分以上(含![]() 分)為及格)與性別有關”?
分)為及格)與性別有關”?
口語成績及格 | 口語成績不及格 | 合計 | |
男生 |
|
| |
女生 |
|
| |
合計 |
|
附臨界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知AB為圓O的直徑,且AB=4,點D為線段AB上一點,且![]() ,點C為圓O上一點,且
,點C為圓O上一點,且![]() .點P在圓O所在平面上的正投影為點D,PD=DB.
.點P在圓O所在平面上的正投影為點D,PD=DB.
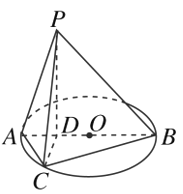
(1)求證:CD⊥平面PAB;
(2)求直線PC與平面PAB所成的角.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com