
【題目】在平面直角坐標系中,圓![]() 的方程為
的方程為![]() (
(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的單位長度,直線
軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的單位長度,直線![]() 的極坐標方程為
的極坐標方程為![]()
(1)當![]() 時,判斷直線
時,判斷直線![]() 與圓
與圓![]() 的關系;
的關系;
(2)當![]() 上有且只有一點到直線
上有且只有一點到直線![]() 的距離等于
的距離等于![]() 時,求
時,求![]() 上到直線
上到直線![]() 距離為
距離為![]() 的點的坐標.
的點的坐標.
 小學奪冠AB卷系列答案
小學奪冠AB卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,準備在墻上釘一個支架,支架由兩直桿AC與BD 焊接而成,焊接點 D 把桿AC 分成 AD, CD 兩段,其中兩固定點A,B 間距離為1 米,AB 與桿 AC 的夾角為60 ,桿AC 長為 1 米,若制作 AD 段的成本為a 元/米,制作 CD 段的成本是 2a 元/米,制作桿BD 成本是 3a 元/米. 設 ADB ,則制作整個支架的總成本記為 S 元.
(1)求S關于 的函數表達式,并求出的取值范圍;
(2)問 ![]() 段多長時,S最小?
段多長時,S最小?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A、B、C所對的邊分別為a、b、c,已知a≠b,cos2A﹣cos2B= ![]() sinAcosA﹣
sinAcosA﹣ ![]() sinBcosB. (Ⅰ)求角C的大小;
sinBcosB. (Ⅰ)求角C的大小;
(Ⅱ)若c= ![]() ,siniA=
,siniA= ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB. 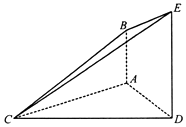
(I)求證:平面BCE⊥平面CDE;
(II)求平面BCE與平面ADEB所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某鄉鎮為了提高當地地方經濟總量,決定引進資金對原有的兩個企業![]() 和
和![]() 進行改造,計劃每年對兩個企業共投資500萬元,要求對每個企業至少投資50萬元.根據已有經驗,改造后
進行改造,計劃每年對兩個企業共投資500萬元,要求對每個企業至少投資50萬元.根據已有經驗,改造后![]() 企業的年收益
企業的年收益![]() (單位:萬元)和
(單位:萬元)和![]() 企業的年收益
企業的年收益![]() (單位:萬元)與投入資金
(單位:萬元)與投入資金![]() (單位:萬元)分別滿足關系式:
(單位:萬元)分別滿足關系式:![]() ,
,![]() .設對
.設對![]() 企業投資額為
企業投資額為![]() (單位:萬元),每年兩個企業的總收益為
(單位:萬元),每年兩個企業的總收益為![]() (單位:萬元).
(單位:萬元).
(1)求![]() ;
;
(2)試問如何安排兩個企業的投入資金,才能使兩個企業的年總收益達到最大,并求出最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=1,an+1=2an+1(n∈N*).
(1)求數列{an}的通項公式;
(2)設Sn為數列{ ![]() }的前n項和,求證:1≤Sn<4.
}的前n項和,求證:1≤Sn<4.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (k為常數,e為自然對數的底數),曲線
(k為常數,e為自然對數的底數),曲線![]() 在點(1, f (1))處的切線與x軸平行.
在點(1, f (1))處的切線與x軸平行.
(1)求k的值;
(2)求![]() 的單調區間;
的單調區間;
(3)設![]() 其中
其中![]() 為
為![]() 的導函數,證明:對任意
的導函數,證明:對任意![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com