
(本小題滿分14分)已知函數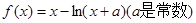 .
.
(1)求函數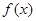 的單調區間;
的單調區間;
(2)當 處取得極值時,若關于
處取得極值時,若關于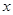 的方程
的方程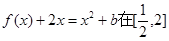 上恰有兩個不相等的實數根,求實數
上恰有兩個不相等的實數根,求實數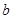 的取值范圍;
的取值范圍;
(3)求證:當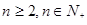 時,有
時,有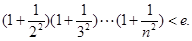
(1)增區間: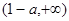 ,減區間:
,減區間: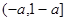 ;
(2)
;
(2)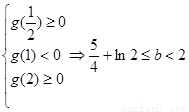
(3)見解析。
【解析】本試題主要是考查了導數在研究函數中的運用,求解函數的單調區間和極值問題以及運用導數證明不等式的問題的綜合運用。
(1)分析定義域,然后求導 ,然后對于導數大于零或者小于零作出討論,得到單調區間。
,然后對于導數大于零或者小于零作出討論,得到單調區間。
(2)因為當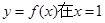 處取得極值時,若關于
處取得極值時,若關于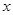 的方程
的方程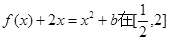 上恰有兩個不相等的實數根,結合函數圖像來得到不等式。
上恰有兩個不相等的實數根,結合函數圖像來得到不等式。
(3)由(1)、(2)可得,當 為增函數
為增函數
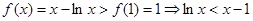 ,然后放縮法得到證明。
,然后放縮法得到證明。
(1)
增區間: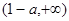 減區間:
減區間: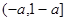 ……………………3分
……………………3分
(2)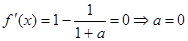
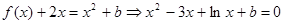
令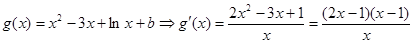
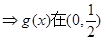 為增函數,
為增函數,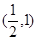 為減函數,
為減函數,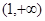 為增函數……………………5分
為增函數……………………5分
則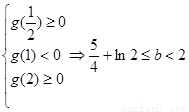 …………………………………………………7分
…………………………………………………7分
(3)由(1)、(2)可得,當 為增函數
為增函數
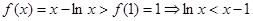 …………………………………………10分
…………………………………………10分
令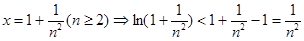 ………………………………12分
………………………………12分
則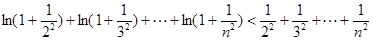
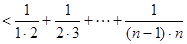 ………………13分
………………13分
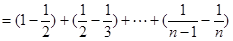

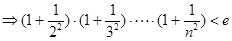 ………………………………………………14分
………………………………………………14分


科目:高中數學 來源: 題型:
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分14分)設橢圓C1的方程為![]() (a>b>0),曲線C2的方程為y=
(a>b>0),曲線C2的方程為y=![]() ,且曲線C1與C2在第一象限內只有一個公共點P。(1)試用a表示點P的坐標;(2)設A、B是橢圓C1的兩個焦點,當a變化時,求△ABP的面積函數S(a)的值域;(3)記min{y1,y2,……,yn}為y1,y2,……,yn中最小的一個。設g(a)是以橢圓C1的半焦距為邊長的正方形的面積,試求函數f(a)=min{g(a), S(a)}的表達式。
,且曲線C1與C2在第一象限內只有一個公共點P。(1)試用a表示點P的坐標;(2)設A、B是橢圓C1的兩個焦點,當a變化時,求△ABP的面積函數S(a)的值域;(3)記min{y1,y2,……,yn}為y1,y2,……,yn中最小的一個。設g(a)是以橢圓C1的半焦距為邊長的正方形的面積,試求函數f(a)=min{g(a), S(a)}的表達式。
查看答案和解析>>
科目:高中數學 來源:2011年江西省撫州市教研室高二上學期期末數學理卷(A) 題型:解答題
(本小題滿分14分)
已知 =2,點(
=2,點( )在函數
)在函數 的圖像上,其中
的圖像上,其中 =
= .
.
(1)證明:數列 }是等比數列;
}是等比數列;
(2)設 ,求
,求 及數列{
及數列{ }的通項公式;
}的通項公式;
(3)記 ,求數列{
,求數列{ }的前n項和
}的前n項和 ,并證明
,并證明 .
.
查看答案和解析>>
科目:高中數學 來源:2015屆山東省威海市高一上學期期末考試數學試卷(解析版) 題型:解答題
(本小題滿分14分)
某網店對一應季商品過去20天的銷售價格及銷售量進行了監測統計發現,第 天(
天( )的銷售價格(單位:元)為
)的銷售價格(單位:元)為 ,第
,第 天的銷售量為
天的銷售量為 ,已知該商品成本為每件25元.
,已知該商品成本為每件25元.
(Ⅰ)寫出銷售額 關于第
關于第 天的函數關系式;
天的函數關系式;
(Ⅱ)求該商品第7天的利潤;
(Ⅲ)該商品第幾天的利潤最大?并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年廣東省高三下學期第一次月考文科數學試卷(解析版) 題型:解答題
(本小題滿分14分)已知 的圖像在點
的圖像在點 處的切線與直線
處的切線與直線 平行.
平行.
⑴ 求 ,
, 滿足的關系式;
滿足的關系式;
⑵ 若 上恒成立,求
上恒成立,求 的取值范圍;
的取值范圍;
⑶ 證明: (
( )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com