
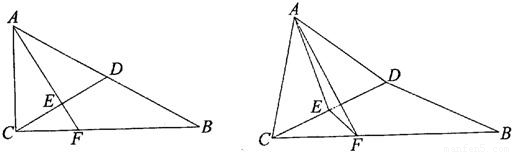
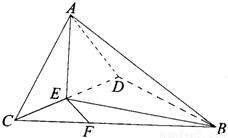
 (I)證明:在Rt△ABC中,D為AB的中點,
(I)證明:在Rt△ABC中,D為AB的中點,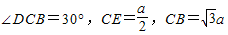 ,
,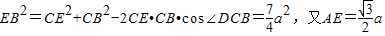 ,
,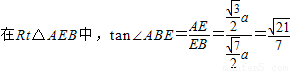 .
.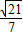 .(14分)
.(14分)

 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:高中數學 來源: 題型:
 如圖,在Rt△ABC中,∠ACB=90°,以AC為直徑的⊙O與AB邊交于點D,過點D作⊙O的切線,交BC于點E.
如圖,在Rt△ABC中,∠ACB=90°,以AC為直徑的⊙O與AB邊交于點D,過點D作⊙O的切線,交BC于點E.| 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于點P.
如圖,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于點P.查看答案和解析>>
科目:高中數學 來源: 題型:
 8.如圖,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如圖,在Rt△ABC中,∠CAB=90°,AB=2,AC=
| ||
| 2 |
| DM |
| DN |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在Rt△ABC中,AC=1,BC=x,D是斜邊AB的中點,將△BCD沿直線CD翻折,若在翻折過程中存在某個位置,使得CB⊥AD,則x的取值范圍是( )
如圖,在Rt△ABC中,AC=1,BC=x,D是斜邊AB的中點,將△BCD沿直線CD翻折,若在翻折過程中存在某個位置,使得CB⊥AD,則x的取值范圍是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com