
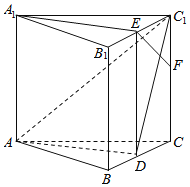
【題目】如圖所示,在正三棱柱ABC-A1B1C1中,已知D,E分別為BC,B1C1的中點,點F在棱CC1上,且EF⊥C1D.求證:
(1)直線A1E∥平面ADC1;
(2)直線EF⊥平面ADC1.

【答案】(1)見解析;(2)見解析
【解析】
(1)先證明A1E∥AD,再證明直線A1E∥平面ADC1;(2)先證明AD⊥EF,EF⊥C1D,再證明直線EF⊥平面ADC1.
(1)連接ED,∵D,E分別為BC,B1C1的中點,
∴B1E∥BD且B1E=BD,
∴四邊形B1BDE是平行四邊形,
∴BB1∥DE且BB1=DE,又BB1∥AA1且BB1=AA1,
∴AA1∥DE且AA1=DE,
∴四邊形AA1ED是平行四邊形,
∴A1E∥AD,又∵A1E平面ADC1,AD平面ADC1,
∴直線A1E∥平面ADC1.
(2)在正三棱柱ABC-A1B1C1中,BB1⊥平面ABC,又AD平面ABC,所以AD⊥BB1,
又△ABC是正三角形,且D為BC的中點,
∴AD⊥BC,又BB1,BC平面B1BCC1,BB1∩BC=B,
∴AD⊥平面B1BCC1,又EF平面B1BCC1,
∴AD⊥EF,
又EF⊥C1D,C1D,AD平面ADC1,C1D∩AD=D,
∴直線EF⊥平面ADC1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 為橢圓
為橢圓![]() 上任一點,
上任一點, ![]() 為其右焦點,點
為其右焦點,點![]() 滿足
滿足![]() .
.
①證明: ![]() 為定值;
為定值;
②設直線![]() 與橢圓
與橢圓![]() 有兩個不同的交點
有兩個不同的交點![]() ,與
,與![]() 軸交于點
軸交于點![]() .若
.若![]() 成等差數列,求
成等差數列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c.已知2cos(B-C)+1=4cosBcosC.
(Ⅰ)求A;
(Ⅱ)若a=2![]() ,△ABC的面積為2
,△ABC的面積為2![]() ,求b+c.
,求b+c.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】最近幾年,每年11月初,黃浦江上漂浮著的水葫蘆便會迅速增長,嚴重影響了市容景觀,為了解決這個環境問題,科研人員進行科研攻關,下圖是科研人員在實驗室池塘中觀察水葫蘆面積與時間的函數關系圖像,假設其函數關系為指數函數,并給出下列說法:

①此指數函數的底數為![]() ;
;
②在第![]() 個月時,水葫蘆的面積會超過
個月時,水葫蘆的面積會超過![]() ;
;
③設水葫蘆面積蔓延至![]() 所需的時間分別為
所需的時間分別為![]() ,則有
,則有![]() ;其中正確的說法有( )
;其中正確的說法有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】流行性感冒多由病毒引起,據調查,空氣月平均相對濕度過大或過小時,都有利于一些病毒繁殖和傳播,科學測定,當空氣月平均相對濕度大于65010或小于![]() 時,有利于病毒繁殖和傳播.下表記錄了某年甲、乙兩個城市12個月的空氣月平均相對濕度.
時,有利于病毒繁殖和傳播.下表記錄了某年甲、乙兩個城市12個月的空氣月平均相對濕度.
第一季度 | 第二季度 | 第三季度 | 第四季度 | |||||||||
1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | |
甲地 |
|
|
|
|
|
|
|
|
|
|
| |
乙地 |
|
|
|
|
|
|
|
|
|
|
|
|
(I)從上表12個月中,隨機取出1個月,求該月甲地空氣月平均相對濕度有利于病毒繁殖和傳播的概率;
(Ⅱ)從上表第一季度和第二季度的6個月中隨機取出2個月,記這2個月中甲、乙兩地空氣月平均相對濕度都有利于病毒繁殖和傳播的月份的個數為![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)若![]() ,設乙地上表12個月的空氣月平均相對濕度的中位數為
,設乙地上表12個月的空氣月平均相對濕度的中位數為![]() ,求
,求![]() 的最大值和最小值.(只需寫出結論)
的最大值和最小值.(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中《方田》章有弧田面積計算問題,計算術曰:以弦乘矢,矢又自乘,并之,二而一.其大意是,弧田面積計算公式為:弧田面積![]() (弦乘矢+矢乘矢),弧田是由圓弧(簡稱為弧田的弧)和以圓弧的端點為端點的線段(簡稱 (弧田的弦)圍成的平面圖形,公式中“弦”指的是弧田的弦長,“矢”等于弧田的弧所在圓的半徑與圓心到弧田的弦的距離之差.現有一弧田,其弦長
(弦乘矢+矢乘矢),弧田是由圓弧(簡稱為弧田的弧)和以圓弧的端點為端點的線段(簡稱 (弧田的弦)圍成的平面圖形,公式中“弦”指的是弧田的弦長,“矢”等于弧田的弧所在圓的半徑與圓心到弧田的弦的距離之差.現有一弧田,其弦長![]() 等于
等于![]() ,其弧所在圓為圓
,其弧所在圓為圓![]() ,若用上述弧田面積計算公式計算得該弧田的面積為
,若用上述弧田面積計算公式計算得該弧田的面積為![]() ,則
,則![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]()
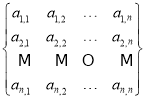 是由
是由![]() 組成的
組成的![]() 行
行![]() 列的數表(每個數恰好出現一次),
列的數表(每個數恰好出現一次),![]() 且
且![]() .
.
若存在![]() ,
, ![]() ,使得
,使得![]() 既是第
既是第![]() 行中的最大值,也是第
行中的最大值,也是第![]() 列中的最小值,則稱數表
列中的最小值,則稱數表![]() 為一個“
為一個“![]() 數表”
數表”![]() 為數表
為數表![]() 的一個“
的一個“![]() 值”,
值”,
對任意給定的![]() ,所有“
,所有“![]() 數表”構成的集合記作
數表”構成的集合記作![]() .
.
判斷下列數表是否是“![]() 數表”.若是,寫出它的一個“
數表”.若是,寫出它的一個“![]() 值”;
值”;
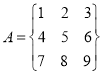 ,
, 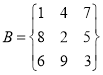
(Ⅱ)求證:若數表![]() 是“
是“![]() 數表”,則
數表”,則![]() 的“
的“![]() 值”是唯一的;
值”是唯一的;
(Ⅲ)在![]() 中隨機選取一個數表
中隨機選取一個數表![]() ,記
,記![]() 的“
的“![]() 值”為
值”為![]() ,求
,求![]() 的數學期望
的數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (a>b>0),以橢圓短軸的一個頂點B與兩個焦點F1,F2為頂點的三角形周長是4+2
(a>b>0),以橢圓短軸的一個頂點B與兩個焦點F1,F2為頂點的三角形周長是4+2![]() ,且∠BF1F2=
,且∠BF1F2=![]() .
.
(1)求橢圓C的標準方程;
(2)若過點Q(1,![]() )引曲線C的弦AB恰好被點Q平分,求弦AB所在的直線方程.
)引曲線C的弦AB恰好被點Q平分,求弦AB所在的直線方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com