
【題目】已知函數![]() .
.
(1)設![]() ,求
,求![]() 的最大值及相應的
的最大值及相應的![]() 值;
值;
(2)對任意正數![]() 恒有
恒有![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)當![]() 時,
時,![]() 取得最大值
取得最大值![]() ;(2)
;(2)![]()
【解析】
(1)先化簡函數g(x)=lnx﹣f′(x)f(x)=lnx﹣(2x﹣1)(x2﹣x),從而求定義域;再求導g′(x)![]() ;從而確定函數的最大值及相應的
;從而確定函數的最大值及相應的![]() 值;
值;
(2)f(x)+f(![]() )≥(x
)≥(x![]() )lnm可化為x2﹣x
)lnm可化為x2﹣x![]() (x
(x![]() )lnm;從而化為lnm
)lnm;從而化為lnm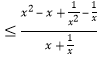 ;化簡得
;化簡得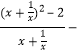 1=(x
1=(x![]() )
)![]() 1;從而利用換元法求函數的最值,從而化恒成立問題為最值問題.
1;從而利用換元法求函數的最值,從而化恒成立問題為最值問題.
(1)∵![]() ,∴
,∴![]() ,
,
∴![]()
![]()
則![]()
∵![]() 的定義域為
的定義域為![]() ,∴
,∴![]()
①當![]() 時,
時,![]() ;②當
;②當![]() 時,
時,![]() ;③當
;③當![]() 時,
時,![]()
因此![]() 在
在![]() 上是增函數,在
上是增函數,在![]() 上是減函數,
上是減函數,
故當![]() 時,
時,![]() 取得最大值
取得最大值![]() .
.
(2)由(1)可知,![]()
不等式![]() 可化為
可化為![]() ①
①
因為![]() ,所以
,所以![]() (當且僅當
(當且僅當![]() 取等號)
取等號)
設![]() ,則把①式可化為
,則把①式可化為![]() ,即
,即![]() (對
(對![]() 恒成立)
恒成立)
令![]() ,此函數在
,此函數在![]() 上是增函數,
上是增函數,
所以![]() 的最小值為
的最小值為![]()
于是![]() ,即
,即![]() .
.


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:高中數學 來源: 題型:
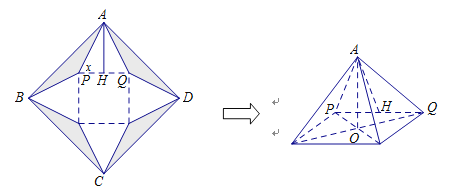
【題目】如圖:設一正方形紙片ABCD邊長為2分米,切去陰影部分所示的四個全等的等腰三角形,剩余為一個正方形和四個全等的等腰三角形,沿虛線折起,恰好能做成一個正四棱錐(粘接損耗不計),圖中![]() ,O為正四棱錐底面中心.
,O為正四棱錐底面中心.
(Ⅰ)若正四棱錐的棱長都相等,求這個正四棱錐的體積V;
(Ⅱ)設等腰三角形APQ的底角為x,試把正四棱錐的側面積S表示為x的函數,并求S的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代數學文化的優秀遺產,數學家劉徽在注解《九章算術》時,發現當圓內接正多邊行的邊數無限增加時,多邊形的面積可無限逼近圓的面積,為此他創立了割圓術,利用割圓術,劉徽得到了圓周率精確到小數點后四位3.1416,后人稱3.14為徽率,如圖是利用劉徽的割圓術設計的程序框圖,若結束程序時,則輸出的![]() 為( )(
為( )(![]() ,
,![]() ,
,![]() )
)

A. 6 B. 12 C. 24 D. 48
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l:![]() 與拋物線C:
與拋物線C:![]() 相切.
相切.
(1)求拋物線方程;
(2)斜率不為0的直線![]() 經過拋物線C的焦點F,交拋物線于兩點A,B,拋物線C上是否存在兩點D,E關于直線
經過拋物線C的焦點F,交拋物線于兩點A,B,拋物線C上是否存在兩點D,E關于直線![]() 對稱.若存在求出斜率k的取值范圍;若不存在,說明理由.
對稱.若存在求出斜率k的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)由0,1,2,…,9這十個數字組成的無重復數字的四位數中,十位數字與千位數字之差的絕對值等于7的四位數的個數共有幾種?
(2)我校高三學習雷鋒志愿小組共有16人,其中一班、二班、三班、四班各4人,現在從中任選3人,要求這三人不能是同一個班級的學生,且在三班至多選1人,求不同的選取法的種數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年是中國改革開放的第40周年,為了充分認識新形勢下改革開放的時代性,某地的民調機構隨機選取了該地的100名市民進行調查,將他們的年齡分成6段:![]() ,并繪制了如圖所示的頻率分布直方圖.
,并繪制了如圖所示的頻率分布直方圖.
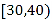
(1)現從年齡在![]() 內的人員中按分層抽樣的方法抽取8人,再從這8人中隨機抽取3人進行座談,用
內的人員中按分層抽樣的方法抽取8人,再從這8人中隨機抽取3人進行座談,用![]() 表示年齡在
表示年齡在![]() 內的人數,求
內的人數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)若用樣本的頻率代替概率,用隨機抽樣的方法從該地抽取20名市民進行調查,其中有![]() 名市民的年齡在
名市民的年齡在![]() 的概率為
的概率為![]() .當
.當![]() 最大時,求
最大時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從學生文藝部6名成員(4男2女)中,挑選2人參加學校舉辦的文藝匯演活動.
(1)求男生甲被選中的概率;
(2)在已知男生甲被選中的條件下,女生乙被選中的概率;
(3)在要求被選中的兩人中必須一男一女的條件下,求女生乙被選中的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com