
(本小題滿分13分)如圖,已知三棱柱 的所有棱長都相等,且側(cè)棱垂直于底面,由
的所有棱長都相等,且側(cè)棱垂直于底面,由 沿棱柱側(cè)面經(jīng)過棱
沿棱柱側(cè)面經(jīng)過棱 到點(diǎn)
到點(diǎn) 的最短路線長為
的最短路線長為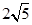 ,設(shè)這條最短路線與
,設(shè)這條最短路線與 的交點(diǎn)為
的交點(diǎn)為 .
.
(1)求三棱柱 的體積;
的體積;
(2)在面 內(nèi)是否存在過
內(nèi)是否存在過 的直線與面
的直線與面 平行?證明你的判斷;
平行?證明你的判斷;
(3)證明:平面 ⊥平面
⊥平面 .
.

平面A1BD內(nèi)存在過點(diǎn)D的直線與平面ABC平行.
【解析】解:(1)如圖,將側(cè)面BB1C1C繞棱CC1旋轉(zhuǎn)120°,
使其與側(cè)面AA1C1C在同一平面上,點(diǎn)B運(yùn)動(dòng)到
點(diǎn)B2的位置,連接A1B2,則A1B2就是由點(diǎn)B沿
棱柱側(cè)面經(jīng)過棱CC1到點(diǎn)A1的最短路線.
設(shè)棱柱的棱長為 ,則B2C=AC=AA1=
,則B2C=AC=AA1= ,
,
∵CD∥AA1 , ∴ 為
為 的中點(diǎn).
………2分
的中點(diǎn).
………2分
在Rt△A1AB2中,由勾股定理得 ,
,
即 ,解得
,解得 ,
∵
,
∵ ,
,
∴ .
………5分
.
………5分
(2)設(shè)A1B與AB1的交點(diǎn)為O,連結(jié)BB2,OD,則 .
.
∵ 平面
平面 ,
, 平面
平面 , ∴
, ∴ 平面
平面 ,
,
即在平面A1BD內(nèi)存在過點(diǎn)D的直線與平面ABC平行. ………9分
(3)連結(jié)AD,B1D ∵ ≌
≌ ≌
≌ ≌
≌ ,
,
∴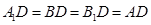 , ∴
, ∴ .
.
∵ ,
, ,
,
∴ 平面A1ABB1 ,又∵
平面A1ABB1 ,又∵ 平面A1BD.
平面A1BD.
∴平面A1BD⊥平面A1ABB1 . ………13分


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2015屆江西省高一第二次月考數(shù)學(xué)試卷(解析版) 題型:解答題
(本小題滿分13分)已知函數(shù)
 .
.
(1)求函數(shù) 的最小正周期和最大值;
的最小正周期和最大值;
(2)在給出的直角坐標(biāo)系中,畫出函數(shù) 在區(qū)間
在區(qū)間 上的圖象.
上的圖象.
(3)設(shè)0<x< ,且方程
,且方程 有兩個(gè)不同的實(shí)數(shù)根,求實(shí)數(shù)m的取值范圍.
有兩個(gè)不同的實(shí)數(shù)根,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年福建省高三年級(jí)八月份月考試卷理科數(shù)學(xué) 題型:解答題
(本小題滿分13分)已知定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052519321600001521/SYS201205251933396875338731_ST.files/image001.png">的函數(shù) 是奇函數(shù).
是奇函數(shù).
(1)求 的值;(2)判斷函數(shù)
的值;(2)判斷函數(shù) 的單調(diào)性;
的單調(diào)性;
(3)若對(duì)任意的 ,不等式恒成立
,不等式恒成立 ,求k的取值范圍.
,求k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年福建省高三年級(jí)八月份月考試卷理科數(shù)學(xué) 題型:解答題
(本小題滿分13分)已知集合 ,
,  ,
, .
.
(1)求 (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:河南省09-10學(xué)年高二下學(xué)期期末數(shù)學(xué)試題(理科) 題型:解答題
(本小題滿分13分)如圖,正三棱柱 的所有棱長都為2,
的所有棱長都為2, 為
為 的中點(diǎn)。
的中點(diǎn)。
(Ⅰ)求證: ∥平面
∥平面 ;
;
(Ⅱ)求異面直線 與
與 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

[來源:KS5
U.COM
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年福建省高三5月月考調(diào)理科數(shù)學(xué) 題型:解答題
(本小題滿分13分)
已知 為銳角,且
為銳角,且 ,函數(shù)
,函數(shù) ,數(shù)列{
,數(shù)列{ }的首項(xiàng)
}的首項(xiàng) .
.
(1) 求函數(shù) 的表達(dá)式;
的表達(dá)式;
(2)在 中,若
中,若 A=2
A=2 ,
, ,BC=2,求
,BC=2,求 的面積
的面積
(3) 求數(shù)列 的前
的前 項(xiàng)和
項(xiàng)和
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com