
【題目】某校辨論隊計劃在周六、周日各參加一場辨論賽,分別由正、副隊長負責,已知該校辯論隊共有10位成員(包含正、副隊長),每場比賽除負責人外均另需3位隊員(同一隊員可同時參加兩天的比賽,正、副隊長只能參加一場比賽).假設正副隊長分別將各自比賽通知的信息獨立、隨機地發給辯論隊8名隊員中的3位,且所發信息都能收到.
(1)求辯論隊員甲收到隊長或副隊長所發比賽通知信息的概率;
(2)記辯論隊收到正副隊長所發比賽通知信息的隊員人數為隨機變量![]() ,求
,求![]() 的分布列及其數學期望.
的分布列及其數學期望.
【答案】(1)![]() ;(2)分布列見解析,
;(2)分布列見解析,![]() .
.
【解析】
(1)根據已知條件甲隊員收到正副隊長的通知信息概率均為![]() ,沒有收到正副隊長的通知信息概率均為
,沒有收到正副隊長的通知信息概率均為![]() ,根據相互獨立同時發生的概率公式,可求出甲隊員沒有收到正隊長也沒收到副隊長所發比賽通知信息的概率,由對立事件的概率關系,即可求解;
,根據相互獨立同時發生的概率公式,可求出甲隊員沒有收到正隊長也沒收到副隊長所發比賽通知信息的概率,由對立事件的概率關系,即可求解;
(2)由題意可得隨機變量![]() 可取值為3,4,5,6,根據古典概型的概率,分別求出
可取值為3,4,5,6,根據古典概型的概率,分別求出![]() 的概率,可得到分布列,按照期望公式,即可得出結論.
的概率,可得到分布列,按照期望公式,即可得出結論.
(1)設事件![]() 表示:辯論隊員甲收到隊長的通知信息,
表示:辯論隊員甲收到隊長的通知信息,
則![]() ,
,![]() ,
,
設事件![]() 表示:辯論隊員甲收到副隊長的通知信息,
表示:辯論隊員甲收到副隊長的通知信息,
則![]() ,
,
設事件![]() 表示;辯論隊員甲收到隊長或副隊長的通知信息,
表示;辯論隊員甲收到隊長或副隊長的通知信息,
則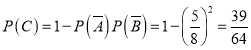 ,
,
所以辯論隊員甲收到隊長或副隊長的通知信息的概率為![]() ;
;
(2)由題意可得隨機變量![]() 可取值為3,4,5,6,
可取值為3,4,5,6,
則![]() ,
,
![]() ,
,![]() ,
,
所以隨機變量![]() 的分布列為:
的分布列為:
| 3 | 4 | 5 | 6 |
|
|
|
|
|
其數學期望![]() .
.


科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象的頂點坐標為
的圖象的頂點坐標為![]() ,且過坐標原點O,數列
,且過坐標原點O,數列![]() 的前n項和為
的前n項和為![]() ,點
,點![]() (
(![]() )在二次函數
)在二次函數![]() 的圖象上.
的圖象上.
(1)求數列![]() 的表達式;
的表達式;
(2)設![]() (
(![]() ),數列
),數列![]() 的前n項和為
的前n項和為![]() ,若
,若![]() 對
對![]() 恒成立,求實數m的取值范圍;
恒成立,求實數m的取值范圍;
(3)在數列![]() 中是否存在這樣的一些項,
中是否存在這樣的一些項,![]() ,
,![]() ,
,![]() ,…
,…![]() ,…(
,…(![]() ),這些項能夠依次構成以
),這些項能夠依次構成以![]() 為首項,q(
為首項,q(![]() ,
,![]() )為公比的等比數列
)為公比的等比數列![]() ?若存在,寫出
?若存在,寫出![]() 關于k的表達式;若不存在,說明理由.
關于k的表達式;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)![]() .
.
(1)求函數y=f(x)的單調區間;
(2)若曲線y=f(x)與直線y=b(b∈R)有3個交點,求實數b的取值范圍;
(3)過點P(﹣1,0)可作幾條直線與曲線y=f(x)相切?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的長軸是短軸的兩倍,以短軸一個頂點和長軸一個頂點為端點的線段作直徑的圓的周長等于
的長軸是短軸的兩倍,以短軸一個頂點和長軸一個頂點為端點的線段作直徑的圓的周長等于![]() ,直線l與橢圓C交于
,直線l與橢圓C交于![]() 兩點,其中直線l不過原點.
兩點,其中直線l不過原點.
(1)求橢圓C的方程;
(2)設直線![]() 的斜率分別為
的斜率分別為![]() ,其中
,其中![]() 且
且![]() .記
.記![]() 的面積為S.分別以
的面積為S.分別以![]() 為直徑的圓的面積依次為
為直徑的圓的面積依次為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
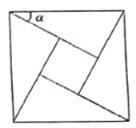
【題目】“劍橋學派”創始人之一數學家哈代說過:“數學家的造型,同畫家和詩人一樣,也應當是美麗的”;古希臘數學家畢達哥拉斯創造的“黃金分割”給我們的生活處處帶來美;我國古代數學家趙爽創造了優美“弦圖”.“弦圖”是由四個全等的直角三角形與一個小正方形拼成的一個大正方形,如果小正方形的面積為1,大正方形的面積為25,直角三角形中較小的銳角為![]() ,則
,則![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為調查學生喜歡“應用統計”課程是否與性別有關,隨機抽取了選修課程的55名學生,得到數據如下表:
喜歡統計課程 | 不喜歡統計課程 | ||
男生 | 20 | 5 | |
女生 | 10 | 20 | |
(1)判斷是否有99.5%的把握認為喜歡“應用統計”課程與性別有關?
(2)用分層抽樣的方法從喜歡統計課程的學生中抽取6名學生作進一步調查,將這6名學生作為一個樣本,從中任選2人,求恰有1個男生和1個女生的概率.
臨界值參考:
| 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在原點的橢圓![]() 和拋物線
和拋物線![]() 有相同的焦點
有相同的焦點![]() ,橢圓
,橢圓![]() 過點
過點![]() ,拋物線
,拋物線![]() 的頂點為原點.
的頂點為原點.
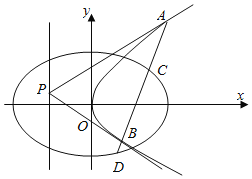
![]() 求橢圓
求橢圓![]() 和拋物線
和拋物線![]() 的方程;
的方程;
![]() 設點P為拋物線
設點P為拋物線![]() 準線上的任意一點,過點P作拋物線
準線上的任意一點,過點P作拋物線![]() 的兩條切線PA,PB,其中A,B為切點.
的兩條切線PA,PB,其中A,B為切點.
![]() 設直線PA,PB的斜率分別為
設直線PA,PB的斜率分別為![]() ,
,![]() ,求證:
,求證:![]() 為定值;
為定值;
![]() 若直線AB交橢圓
若直線AB交橢圓![]() 于C,D兩點,
于C,D兩點,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的面積,試問:
的面積,試問:![]() 是否有最小值?若有,求出最小值;若沒有,請說明理由.
是否有最小值?若有,求出最小值;若沒有,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2022年北京冬奧會的申辦成功與“3億人上冰雪”口號的提出,將冰雪這個冷項目迅速炒“熱”.北京某綜合大學計劃在一年級開設冰球課程,為了解學生對冰球運動的興趣,隨機從該校一年級學生中抽取了100人進行調查,其中女生中對冰球運動有興趣的占![]() ,而男生有10人表示對冰球運動沒有興趣額.
,而男生有10人表示對冰球運動沒有興趣額.
(1)完成![]() 列聯表,并回答能否有
列聯表,并回答能否有![]() 的把握認為“對冰球是否有興趣與性別有關”?
的把握認為“對冰球是否有興趣與性別有關”?
有興趣 | 沒興趣 | 合計 | |
男 | 55 | ||
女 | |||
合計 |
(2)已知在被調查的女生中有5名數學系的學生,其中3名對冰球有興趣,現在從這5名學生中隨機抽取3人,求至少有2人對冰球有興趣的概率.
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知橢圓C:![]() 的短軸長為2,傾斜角為
的短軸長為2,傾斜角為![]() 的直線l與橢圓C相交于A,B兩點,線段AB的中點為M,且點M與坐標原點O連線的斜率為
的直線l與橢圓C相交于A,B兩點,線段AB的中點為M,且點M與坐標原點O連線的斜率為![]() .
.
(1)求橢圓C的標準方程;
(2)若![]() ,P是以AB為直徑的圓上的任意一點,求證:
,P是以AB為直徑的圓上的任意一點,求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com