
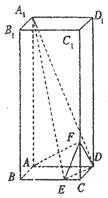
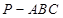 中,
中,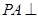 底面
底面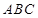 ,
,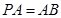 ,
,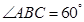 ,
,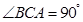 ,點
,點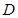 ,
,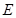 分別在棱
分別在棱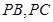 上,且
上,且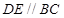
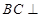 平面
平面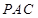 ;
;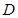 為
為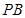 的中點時,求
的中點時,求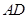 與平面
與平面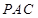 所成的角的大小;
所成的角的大小;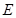 使得二面角
使得二面角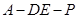 為直二面角?并說明理由.
為直二面角?并說明理由.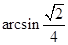 (Ⅲ)存在,理由見解析
(Ⅲ)存在,理由見解析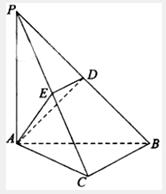
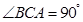 ,∴AC⊥BC.
,∴AC⊥BC.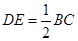 ,
,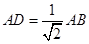 ,∴在Rt△ABC中,
,∴在Rt△ABC中,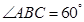 ,∴
,∴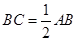 .
.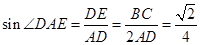 ,∴
,∴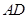 與平面
與平面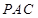 所成的角的大小
所成的角的大小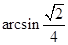 .
.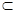 平面PAC,PE
平面PAC,PE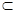 平面PAC,∴DE⊥AE,DE⊥PE,∴∠AEP為二面角
平面PAC,∴DE⊥AE,DE⊥PE,∴∠AEP為二面角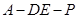 的平面角,
的平面角,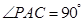 .∴在棱PC上存在一點E,使得AE⊥PC,這時
.∴在棱PC上存在一點E,使得AE⊥PC,這時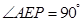 ,
,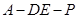 是直二面角.
是直二面角.

 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案 課堂練加測系列答案
課堂練加測系列答案科目:高中數(shù)學 來源:不詳 題型:單選題
A. | B.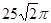 | C.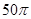 | D.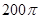 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
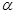 ,
,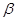 ,
,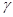 是三個互不重合的平面,
是三個互不重合的平面,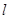 是一條直線,下列命題中正確命題是( )
是一條直線,下列命題中正確命題是( )A.若 , ,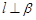 ,則 ,則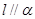 | B.若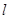 上有兩個點到 上有兩個點到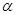 的距離相等,則 的距離相等,則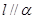 |
C.若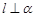 , ,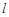 ∥ ∥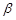 ,則 ,則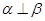 | D.若 , ,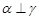 ,則 ,則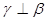 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
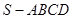 的底面邊長為2,高為2,
的底面邊長為2,高為2,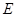 為邊
為邊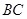 的中點,動點
的中點,動點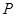 在表面上運動,并且總保持
在表面上運動,并且總保持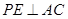 ,則動點
,則動點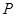 的軌跡的周長為( )
的軌跡的周長為( )
A.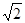 | B.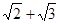 | C.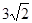 | D.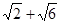 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
 --
-- ,E、F分別是
,E、F分別是 、
、 的中點,p是
的中點,p是 上的動點(包括端點),過E、D、P作正方體的截面,若截面為四邊形,則P的軌跡是
上的動點(包括端點),過E、D、P作正方體的截面,若截面為四邊形,則P的軌跡是 B、線段
B、線段
 和一點
和一點 D、線段
D、線段 和一點C
和一點C查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
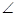 BCD=60
BCD=60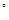 ,E是CD的中點,PA
,E是CD的中點,PA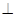 底面ABCD,PA=2.
底面ABCD,PA=2.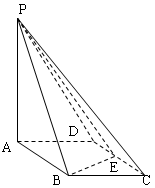
 平面PAB;
平面PAB;查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com