
 解:(1)由題意知這個抽樣是按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,是一個具有相同間隔的抽樣,并且總體的個數比較多,這是一個系統抽樣.
解:(1)由題意知這個抽樣是按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,是一個具有相同間隔的抽樣,并且總體的個數比較多,這是一個系統抽樣. .(13分)
.(13分)

 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
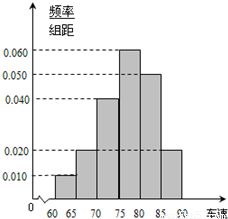
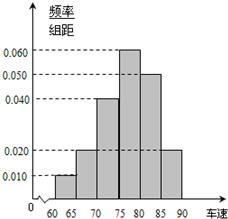 2012年“雙節”期間,高速公路車輛較多.某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(km/h)分成六段:[60,65)[65,70)[70,75)[75,80),[80,85)[85,90),得到如圖的頻率分布直方圖.問:
2012年“雙節”期間,高速公路車輛較多.某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(km/h)分成六段:[60,65)[65,70)[70,75)[75,80),[80,85)[85,90),得到如圖的頻率分布直方圖.問:查看答案和解析>>
科目:高中數學 來源: 題型:
 2012年“雙節”期間,高速公路車輛較多.某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(km/t)分成六段:(60,65),[65,70),[70,75),[80,85),[85,90)后得到如圖的頻率分布直方圖.
2012年“雙節”期間,高速公路車輛較多.某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(km/t)分成六段:(60,65),[65,70),[70,75),[80,85),[85,90)后得到如圖的頻率分布直方圖.查看答案和解析>>
科目:高中數學 來源: 題型:
 2012年“雙節”期間,高速公路車輛較多.某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(km/t)分成六段:[60,65),[65,70)[70,75),[75,80),[80,85),[85,90)后得到如圖5的頻率分布直方圖.
2012年“雙節”期間,高速公路車輛較多.某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(km/t)分成六段:[60,65),[65,70)[70,75),[75,80),[80,85),[85,90)后得到如圖5的頻率分布直方圖.查看答案和解析>>
科目:高中數學 來源:2013-2014學年湖南省益陽市高三第一次模擬考試理數學試卷(解析版) 題型:解答題
在2012年“雙節”期間,高速公路車輛較多。某調查公司在一服務區從七座以下小型汽車中,按進服務區的先后每間隔50輛就抽取一輛的抽樣方法,抽取了40名駕駛員進行調查,將他們在某段高速公路上的車速(km/t)分成6段: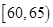 ,
,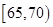 ,
, ,
,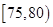 ,
,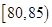 ,
,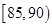 后得到如圖的頻率分布直方圖。問:
后得到如圖的頻率分布直方圖。問:
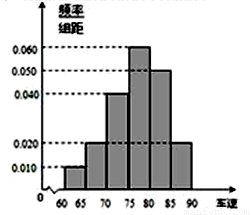
(1)該公司在調查取樣中,用到的是什么抽樣方法?
(2)求這40輛小型汽車車速的眾數和中位數的估計值;
(3)若從車速在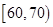 中的車輛中任取2輛,求抽出的2輛中速度在
中的車輛中任取2輛,求抽出的2輛中速度在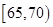 中的車輛數
中的車輛數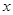 的分布列及其數學期望。(12分)
的分布列及其數學期望。(12分)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com