
【題目】已知函數(shù)![]() ,
,![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)若函數(shù)![]() 的圖象與直線
的圖象與直線![]() 交于
交于![]() 兩點,線段
兩點,線段![]() 中點的橫坐標(biāo)為
中點的橫坐標(biāo)為![]() ,證明:
,證明: ![]() 為函數(shù)
為函數(shù)![]() 的導(dǎo)函數(shù)).
的導(dǎo)函數(shù)).
【答案】(1) 當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,當(dāng)
上單調(diào)遞增,當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增,當(dāng)
上單調(diào)遞增,當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減;(2)證明見解析.
上單調(diào)遞減;(2)證明見解析.
【解析】
試題分析:(1)借助題設(shè)條件運用導(dǎo)數(shù)與函數(shù)的單調(diào)性的關(guān)系與分類整合思想求解;(2)依據(jù)題設(shè)構(gòu)造函數(shù)運用導(dǎo)數(shù)知識推證.
試題解析:
(1)由題可知,![]() . ①當(dāng)
. ①當(dāng)![]() 時,
時,
令![]() ,則
,則![]() ,令
,令![]() ,則
,則![]() .
.
②當(dāng)![]() 時,
時,![]() .③當(dāng)
.③當(dāng)![]() 時,令
時,令![]() ,則
,則![]() ,令
,令![]() ,則
,則![]() ,綜上,①當(dāng)
,綜上,①當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增;②當(dāng)
上單調(diào)遞增;②當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增;③當(dāng)
上單調(diào)遞增;③當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減.
上單調(diào)遞減.
(2)
![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 時,
時,
![]() 在
在![]() 上單調(diào)遞增,與
上單調(diào)遞增,與![]() 軸不可能有兩個交點,故
軸不可能有兩個交點,故![]() .
.
當(dāng)![]() 時,令
時,令![]() ,則
,則![]() ;令
;令![]() ,則
,則![]() .
.
故![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減.不妨設(shè)
上單調(diào)遞減.不妨設(shè)![]() ,
,
且![]() .要證
.要證![]() ,需證
,需證![]() ,
,
即證![]() ,
,
又![]() ,所以只需證
,所以只需證![]() .
.
即證:當(dāng)![]() 時,
時,![]() .
.
設(shè)![]() ,
,
則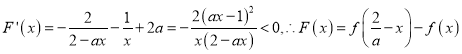 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
又![]() ,故
,故![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知各項均不相等的等差數(shù)列![]() 的前五項和
的前五項和![]() ,且
,且![]() 成等比數(shù)列.
成等比數(shù)列.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)若![]() 為數(shù)列
為數(shù)列![]() 的前
的前![]() 項和,且存在
項和,且存在![]() ,使得
,使得![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知橢圓![]() 的長軸長是短軸長的
的長軸長是短軸長的![]() 倍,右焦點為
倍,右焦點為![]() ,點
,點![]() 分別是該橢圓的上、下頂點,點
分別是該橢圓的上、下頂點,點![]() 是直線
是直線![]() 上的一個動點(與
上的一個動點(與![]() 軸交點除外),直線
軸交點除外),直線![]() 交橢圓于另一點
交橢圓于另一點![]() ,記直線
,記直線![]() ,
, ![]() 的斜率分別為
的斜率分別為![]()

(1)當(dāng)直線![]() 過點
過點![]() 時,求
時,求![]() 的值;
的值;
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖是我國2008年至2014年生活垃圾無害化處理量(單位:億噸)的折線圖.
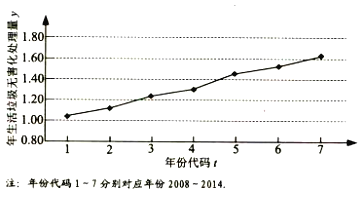
(Ⅰ)由折線圖看出,可用線性回歸模型擬合![]() 與
與![]() 的關(guān)系,請用相關(guān)系數(shù)加以說明;
的關(guān)系,請用相關(guān)系數(shù)加以說明;
(Ⅱ)建立![]() 關(guān)于
關(guān)于![]() 的回歸方程(系數(shù)精確到0.01),預(yù)測2016年我國生活垃圾無害化處理量.
的回歸方程(系數(shù)精確到0.01),預(yù)測2016年我國生活垃圾無害化處理量.
參考數(shù)據(jù): ![]() ,
, ![]() ,
, 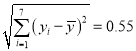 ,
, ![]() .
.
參考公式:相關(guān)系數(shù)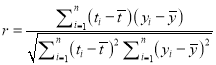 ,
,
回歸方程![]() ,
, 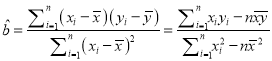 ,
,
本題中斜率和截距的最小二乘估計公式分別為: 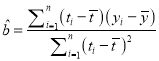 ,
, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
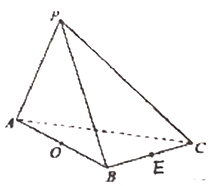
【題目】在三棱錐![]() 中,
中, ![]() 和
和![]() 是邊長為
是邊長為![]() 的等邊三角形,
的等邊三角形, ![]() ,
, ![]() 是
是![]() 中點,
中點, ![]() 是
是![]() 中點.
中點.
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(Ⅲ)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 的余弦值為
的余弦值為![]() ?若存在,指出點
?若存在,指出點![]() 在
在![]() 上的位置;若不存在,說明理由.
上的位置;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
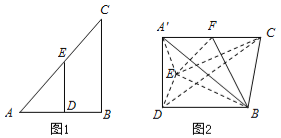
【題目】如圖1在![]() △
△![]() 中,
中,![]()
![]() ,
,![]() 、
、![]() 分別為線段
分別為線段![]() 、
、![]() 的中點,
的中點,![]() ,
,![]() .以
.以![]() 為折痕,將
為折痕,將![]() △
△![]() 折起到圖2的位置,使平面
折起到圖2的位置,使平面![]() ⊥平面
⊥平面![]() ,連接
,連接![]() ,
,![]() ,設(shè)
,設(shè)![]() 是線段
是線段![]() 上的動點,滿足
上的動點,滿足![]() .
.
(1)證明:平面![]() ⊥平面
⊥平面![]() ;
;
(2)若二面角![]() 的大小為
的大小為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某單位從一所學(xué)校招收某類特殊人才,對20位已經(jīng)選拔入圍的學(xué)生進行運動協(xié)調(diào)能力和邏輯思維能力的測試,其測試結(jié)果如下表:
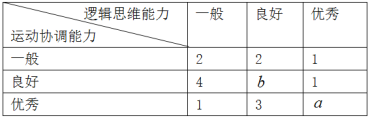
例如表中運動協(xié)調(diào)能力良好且邏輯思維能力一般的學(xué)生是4人,由于部分?jǐn)?shù)據(jù)丟失,只知道從這20位參加測試的學(xué)生中隨機抽取一位,抽到邏輯思維能力優(yōu)秀的學(xué)生的概率為![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
(2)從運動協(xié)調(diào)能力為優(yōu)秀的學(xué)生中任意抽取2位,求其中至少有一位邏輯思維能力優(yōu)秀的學(xué)生的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知曲線![]()
若![]() ,過點
,過點![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的方程;
的方程;
若曲線![]() 表示圓,且直線
表示圓,且直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,是否存在實數(shù)
兩點,是否存在實數(shù)![]() ,使得以
,使得以![]() 為直徑的圓過原點,若存在,求出實數(shù)
為直徑的圓過原點,若存在,求出實數(shù)![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)甲、乙、丙三個乒乓球協(xié)會的運動員人數(shù)分別為27,9,18,先采用分層抽樣的方法從這三個協(xié)會中抽取6名運動員參加比賽.
(Ⅰ)求應(yīng)從這三個協(xié)會中分別抽取的運動員人數(shù);
(Ⅱ)將抽取的6名運動員進行編號,編號分別為![]() ,從這6名運動員中隨機抽取2名參加雙打比賽.
,從這6名運動員中隨機抽取2名參加雙打比賽.
(ⅰ)用所給編號列出所有可能的結(jié)果;
(ⅱ)設(shè)![]() 為事件“編號為
為事件“編號為![]() 的兩名運動員至少有一人被抽到”,求事件
的兩名運動員至少有一人被抽到”,求事件![]() 發(fā)生的概率.
發(fā)生的概率.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com