
【題目】如果數列![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ,且
,且![]() ),滿足:①
),滿足:①![]() ,
,![]() ;
;
②![]() ,那么稱數列
,那么稱數列![]() 為“
為“![]() ”數列.
”數列.
(![]() )已知數列
)已知數列![]() ,
,![]() ,
,![]() ,
,![]() ;數列
;數列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .試判斷數列
.試判斷數列![]() ,
,![]() 是否為“
是否為“![]() ”數列.
”數列.
(![]() )是否存在一個等差數列是“
)是否存在一個等差數列是“![]() ”數列?請證明你的結論.
”數列?請證明你的結論.
(![]() )如果數列
)如果數列![]() 是“
是“![]() ”數列,求證:數列
”數列,求證:數列![]() 中必定存在若干項之和為
中必定存在若干項之和為![]() .
.
【答案】(![]() )數列
)數列![]() 不是“
不是“![]() ”數列,數列
”數列,數列![]() 是“
是“![]() ”數列;(
”數列;(![]() )不存在等差數列是“
)不存在等差數列是“![]() ”數列;(
”數列;(![]() )證明見解析.
)證明見解析.
【解析】分析:(1)根據定義直接判斷即可得解;(2)假設存在等差數列是“![]() ”數列,由
”數列,由![]() ,得
,得![]() ,與
,與![]() 矛盾,從而可證不存在等差數列為“
矛盾,從而可證不存在等差數列為“![]() ”數列;(3)將數列
”數列;(3)將數列![]() 按以下方法重新排列:設
按以下方法重新排列:設![]() 為重新排列后所得數列的前
為重新排列后所得數列的前![]() 項和(
項和(![]() 且
且![]() ),任取大于0的一項作為第一項,則滿足
),任取大于0的一項作為第一項,則滿足![]() ,然后利用反證法,證明即可.
,然后利用反證法,證明即可.
詳解:(![]() )由題目是
)由題目是![]() 定義可直接判斷出,數列
定義可直接判斷出,數列![]() 不符合
不符合![]() 數列要求,數列
數列要求,數列![]() 是“
是“![]() ”數列.
”數列.
(![]() )不存在一個等差數列是“
)不存在一個等差數列是“![]() ”數列,
”數列,
證明:假設存在等差數列是“![]() ”數列,
”數列,
則由![]() ,得
,得![]() 與
與![]() 矛盾,
矛盾,
說明假設不成立,即不存在等差數列是“![]() ”數列.
”數列.
(![]() )將數列
)將數列![]() 按以下方法重新排列:
按以下方法重新排列:
設![]() 為重新排列后所得數列的前
為重新排列后所得數列的前![]() 項和(
項和(![]() ,且
,且![]() ),
),
任取大于![]() 的一項作為第一項,則滿足
的一項作為第一項,則滿足![]() ,
,
假設當![]() 時,
時,![]() ,
,
若![]() ,則任取大于
,則任取大于![]() 的一項作為第
的一項作為第![]() 項,可保證
項,可保證![]() ,
,
若![]() ,則剩下的項必有
,則剩下的項必有![]() 或與
或與![]() 異號的一項,否則總和不是
異號的一項,否則總和不是![]() ,
,
∴取![]() 或與
或與![]() 異號的一項作為第
異號的一項作為第![]() 項,可保證
項,可保證![]() ,
,
如果按上述排列后存在![]() 成立,那么命題得證,
成立,那么命題得證,
否則![]() ,
,![]() ,
,![]()
![]() 這
這![]() 個整數只能取區間
個整數只能取區間![]() 內的非
內的非![]() 整數,
整數,
∵區間![]() 內的非
內的非![]() 整數至多
整數至多![]() 個,
個,
∴一定存在![]() ,
,
那么從第![]() 項到第
項到第![]() 項之和為
項之和為![]() ,命題得證,
,命題得證,
綜上所述,數列![]() 中一定存在若干項之和為
中一定存在若干項之和為![]() ,證畢.
,證畢.


科目:高中數學 來源: 題型:
【題目】已知命題![]() 函數
函數![]() 是
是![]() 上的奇函數,命題
上的奇函數,命題![]() 函數
函數![]() 的定義域和值域都是
的定義域和值域都是![]() ,其中
,其中![]() .
.
(1)若命題![]() 為真命題,求實數
為真命題,求實數![]() 的值;
的值;
(2)若“![]() 且
且![]() ”為假命題,“
”為假命題,“![]() 或
或![]() ”為真命題,求實數
”為真命題,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場舉行有獎促銷活動,顧客購買一定金額的商品后即可參加一次抽獎.隨著抽獎活動的有效開展,參與抽獎活動的人數越來越多,該商場對前5天抽獎活動的人數進行統計,y表示第x天參加抽獎活動的人數,得到統計表如下:
x | 1 | 2 | 3 | 4 | 5 |
y | 50 | 60 | 70 | 80 | 100 |
經過進一步統計分析,發現y與x具有線性相關關系.
(1)若從這5天隨機抽取兩天,求至少有1天參加抽獎人數超過70的概率;
(2)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程![]() ,并估計該活動持續7天,共有多少名顧客參加抽獎?
,并估計該活動持續7天,共有多少名顧客參加抽獎?
參考公式及數據: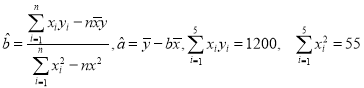 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}的前n項和是Sn , 且Sn+ ![]() an=1,數列{bn},{cn}滿足bn=log3
an=1,數列{bn},{cn}滿足bn=log3 ![]() ,cn=
,cn= ![]() . (Ⅰ)求數列{an}的通項公式;
. (Ⅰ)求數列{an}的通項公式;
(Ⅱ)數列{cn}的前n項和為Tn , 若不等式Tn<m對任意的正整數n恒成立,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四邊形BFED是以BD為直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD. (Ⅰ)求證:AD⊥平面BFED;
(Ⅱ)在線段EF上是否存在一點P,使得平面PAB與平面ADE所成的銳二面角的余弦值為 ![]() .若存在,求出點P的位置;若不存在,說明理由.
.若存在,求出點P的位置;若不存在,說明理由.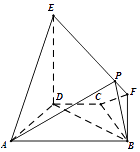
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=alnx+ ![]() x2﹣ax(a為常數)有兩個極值點.
x2﹣ax(a為常數)有兩個極值點.
(1)求實數a的取值范圍;
(2)設f(x)的兩個極值點分別為x1 , x2 , 若不等式f(x1)+f(x2)<λ(x1+x2)恒成立,求λ的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的前n項和為Sn , 且滿足S4=24,S7=63. (Ⅰ)求數列{an}的通項公式;
(Ⅱ)若 ![]() ,求數列{bn}的前n項和Tn .
,求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin2x+2sinxcosx+3cos2x. (Ⅰ)求函數f(x)的單調遞增區間;
(Ⅱ)若x∈[0, ![]() ],求函數f(x)的最值及相應x的取值.
],求函數f(x)的最值及相應x的取值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com