Question

下列五個命題：

①方程y=kx+2可表示經過點(0，2)的所有直線；

②經過點(x₀, y₀)且與直線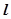:Ax+By+C=0(A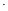B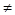0)垂直的直線方程為: B(x－x₀)－A(y－y₀)=0; 

③經過點(x₀, y₀)且與直線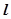:Ax+By+C=0(A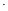B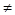0)平行的直線方程為: A(x－x₀)+B(y－y₀)=0;

④存在這樣的直線，既不與坐標軸平行又不經過任何整點;

⑤存在無窮多直線只經過一個整點.

其中真命題是_____________(把你認為正確的命題序號都填上)

 

Answer 1

【答案】

②③④⑤

【解析】

試題分析：①方程y=kx+2可表示經過點(0，2)的所有直線；不正確，不包括y軸。

根據兩直線垂直的條件知，②經過點(x₀, y₀)且與直線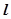:Ax+By+C=0(A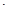B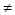0)垂直的直線方程為: B(x－x₀)－A(y－y₀)=0;正確。

根據兩直線平行的條件知，③經過點(x₀, y₀)且與直線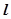:Ax+By+C=0(A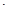B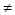0)平行的直線方程為: A(x－x₀)+B(y－y₀)=0;正確。

④存在這樣的直線，既不與坐標軸平行又不經過任何整點;正確，如。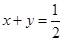

⑤存在無窮多直線只經過一個整點.正確，如直線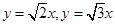……只經過整點（0,0）.

故答案為②③④⑤。

考點：本題主要考查直線方程的各種形式。

點評：中檔題，本題全面考查直線方程的各種形式。說明命題正確，應有結論支持或能推證，說明命題不正確，舉一反例即可。