【題目】2019年11月18日國際射聯步手槍世界杯總決賽在莆田市綜合體育館開幕，這是國際射聯步手槍世界杯總決賽時隔10年再度走進中國.為了增強趣味性，并實時播報現場賽況，我校現場小記者李明和播報小記者王華設計了一套播報轉碼法，發送方由明文→密文（加密），接受方由密文→明文（解密），已知加密的方法是：密碼把英文的明文（真實文）按字母分解，其中英文的
的26個字母（不論大小寫）依次對應1，2，3，…，26這26個自然數通過變換公式：
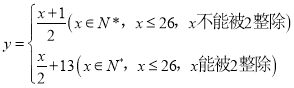，將明文轉換成密文，如
，即
變換成
，即
變換成
.若按上述規定，若王華收到的密文是
，那么原來的明文是（ ）
A.
B.
C.
D.
科目：高中數學 來源： 題型：
【題目】對于各項均為正數的無窮數列
，記
，給出下列定義：
①若存在實數
，使
成立，則稱數列為“有上界數列”；
②若數列為有上界數列，且存在
，使
成立，則稱數列為“有最大值數列”；
③若
，則稱數列為“比減小數列”．
（1）根據上述定義，判斷數列
是何種數列？
（2）若數列中，
，
，求證：數列既是有上界數列又是比減小數列；
（3）若數列是單調遞增數列，且是有上界數列，但不是有最大值數列，求證：
，
．
查看答案和解析>>
科目：高中數學 來源： 題型：
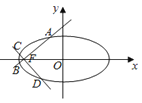
【題目】已知橢圓
經過點
，其左焦點為
.過
點的直線
交橢圓于
、
兩點，交
軸的正半軸于點
.
（1）求橢圓
的方程；
（2）過點且與垂直的直線交橢圓于
、
兩點，若四邊形
的面積為
，求直線的方程；
（3）設
，
，求證：
為定值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的右焦點為
，且點
在橢圓C上.
（1）求橢圓C的標準方程；
（2）過橢圓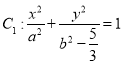
上異于其頂點的任意一點Q作圓
的兩條切線，切點分別為
不在坐標軸上），若直線
在x軸，y軸上的截距分別為
，證明：
為定值；
（3）若
是橢圓
上不同兩點，
軸，圓E過，且橢圓
上任意一點都不在圓E內，則稱圓E為該橢圓的一個內切圓，試問：橢圓是否存在過焦點F的內切圓？若存在，求出圓心E的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】等比數列{an}的各項均為正數，且2a1＋3a2＝1， 
＝9a2a6.
(1)求數列{an}的通項公式；
(2)設bn＝log3a1＋log3a2＋…＋log3an，求數列
的前n項和．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
，對于項數為
的有窮數列
，令
為
中最大值，稱數列
為數列的“創新數列”.例如數列3，5，4，7的創新數列為3，5，5，7. 考查正整數1，2，…，
的所有排列，將每種排列都視為一個有窮數列
.
（1）若
，寫出創新數列為3，4，4，4的所有數列；
（2）是否存在數列的創新數列為等比數列？若存在，求出符合條件的的創新數列；若不存在，請說明理由.
（3）是否存在數列，使它的創新數列為等差數列？若存在，求出滿足所有條件的數列的個數；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，點
滿足方程
.
（1）求點M的軌跡C的方程；
（2）作曲線C關于
軸對稱的曲線，記為
，在曲線C上任取一點
，過點P作曲線C的切線l，若切線l與曲線交于A，B兩點，過點A，B分別作曲線的切線
，證明的交點必在曲線C上.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司生產的某批產品的銷售量
萬件（生產量與銷售量相等）與促銷費用
萬元滿足
（其中
，
為正常數）．已知生產該產品還需投入成本
萬元（不含促銷費用），產品的銷售價格定為
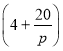元
件．
（1）將該產品的利潤
萬元表示為促銷費用萬元的函數；
（2）促銷費用投入多少萬元時，該公司的利潤最大？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
