【題目】已知
是無窮等比數列，若的每一項都等于它后面所有項的
倍，則實數的取值范圍是______.
【答案】（﹣∞，﹣2]∪（0，+∞）．
【解析】
無窮等比數列{an}的各項和為A，前n項和為Sn，公比為q，0＜|q|≤1，q≠1．可得A
，Sn
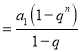，由題意可得：an＝k（A﹣Sn），代入化為：k
，分類討論即可得出．
解：無窮等比數列{an}的各項和為A，前n項和為Sn，公比為q，0＜|q|≤1，q≠1．
則A，Sn，
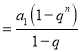由題意可得：an＝k（A﹣Sn），
∴a1q＝k（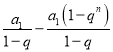
），
化為：k，
1＞q＞0時，k＞0，n→+∞時，k→+∞．
﹣1≤q＜0時，可得：n為偶數時，k∈（﹣∞，﹣2]；n為奇數時，k＞0．
∴k∈（﹣∞，﹣2]∪（0，+∞）．
綜上可得：k∈（﹣∞，﹣2]∪（0，+∞）．
故答案為：（﹣∞，﹣2]∪（0，+∞）．
科目：高中數學 來源： 題型：
【題目】已知
，
，對任意
，有
成立.
（1）求
的通項公式；
（2）設
，
，
是數列
的前
項和，求正整數
，使得對任意，
恒成立；
（3）設
，
是數列
的前項和，若對任意均有
恒成立，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，某小區為美化環境，準備在小區內的草坪的一側修建一條直路OC，另一側修建一條休閑大道.休閑大道的前一段OD是函數
的圖象的一部分，后一段DBC是函數
的圖象，圖象的最高點為
，且
，垂足為點F.
（1）求函數
的解析式；
（2）若在草坪內修建如圖所示的矩形兒童樂園PMFE，點P在曲線OD上，其橫坐標為
，點E在OC上，求兒童樂園的面積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如表提供了工廠技術改造后某種型號設備的使用年限
和所支出的維修費
（萬元）的幾組對照數據：
| 2 | 3 | 4 | 5 | 6 |
| 1 | 2.5 | 3 | 4 | 4.5 |
參考公式：
，
.
（1）若知道對呈線性相關關系，請根據上表提供的數據，用最小二乘法求出關于的線性回歸方程
；
（2）已知該工廠技術改造前該型號設備使用10年的維修費用為9萬元，試根據（1）求出的線性回歸方程，預測該型號設備技術改造后，使用10年的維修費用能否比技術改造前降低？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】運貨卡車以每小時x千米的速度勻速行駛130千米，按交通法規限制50≤x≤100(單位：千米/時).假設汽油的價格是每升2元，而汽車每小時耗油
升，司機的工資是每小時14元.
(1)求這次行車總費用y關于x的表達式；
(2)當x為何值時，這次行車的總費用最低，并求出最低費用的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，直線l的參數方程為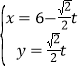
（t是參數），在以坐標原點為極點，x軸的正半軸為極軸的極坐標系中，曲線C的極坐標方程為
．
（Ⅰ）寫出直線l的普通方程、曲線C的參數方程；
（Ⅱ）過曲線C上任意一點A作與直線l的夾角為45°的直線，設該直線與直線l交于點B，求
的最值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】雙曲線
的左、右焦點為
，
，
為右支上的動點（非頂點），
為
的內心.當變化時，的軌跡為（ ）
A.直線的一部分B.橢圓的一部分
C.雙曲線的一部分D.無法確定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
