
【題目】在矩形ABCD中,AB=1,AD=2,動點P在以點C為圓心且與BD相切的圓上.若![]() =
=![]()
![]() +
+![]()
![]() ,則
,則![]() +
+![]() 的最大值為__________.
的最大值為__________.
【答案】![]()
【解析】分析:如圖:以A為原點,以AB,AD所在的直線為x,y軸建立如圖所示的坐標系,先求出圓的標準方程,再設點P的坐標為(![]() cosθ+1,
cosθ+1,![]() sinθ+2),根據
sinθ+2),根據![]() =λ
=λ![]() +μ
+μ![]() ,求出λ,μ,根據三角函數的性質即可求出最值.
,求出λ,μ,根據三角函數的性質即可求出最值.
詳解:如圖:以A為原點,以AB,AD所在的直線為x,y軸建立如圖所示的坐標系,
則A(0,0),B(1,0),D(0,2),C(1,2),
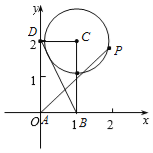
∵動點P在以點C為圓心且與BD相切的圓上,
設圓的半徑為r,
∵BC=2,CD=1,
∴BD=![]() =
=![]()
∴![]() BCCD=
BCCD=![]() BDr,
BDr,
∴r=![]() ,
,
∴圓的方程為(x﹣1)2+(y﹣2)2=![]() ,
,
設點P的坐標為(![]() cosθ+1,
cosθ+1,![]() sinθ+2),
sinθ+2),
∵![]() =λ
=λ![]() +μ
+μ![]() ,
,
∴(![]() cosθ+1,
cosθ+1,![]() sinθ+2)=λ(1,0)+μ(0,2)=(λ,2μ),
sinθ+2)=λ(1,0)+μ(0,2)=(λ,2μ),
∴![]() cosθ+1=λ,
cosθ+1=λ,![]() sinθ+2=2μ,
sinθ+2=2μ,
∴λ+μ=![]() cosθ+
cosθ+![]() sinθ+2=sin(θ+φ)+2,其中tanφ=2,
sinθ+2=sin(θ+φ)+2,其中tanφ=2,
∵﹣1≤sin(θ+φ)≤1,
∴1≤λ+μ≤3,
故λ+μ的最大值為3,
故答案為:3.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知點A(1,2),過點P(5,﹣2)的直線與拋物線y2=4x相交于B,C兩點,則△ABC是( )
A.直角三角形
B.鈍角三角形
C.銳角三角形
D.不能確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為普及高中生安全逃生知識與安全防護能力,某學校高一年級舉辦了高中生安全知識與安全逃生能力競賽.該競賽分為預賽和決賽兩個階段,預賽為筆試,決賽為技能比賽.先將所有參賽選手參加筆試的成績(得分均為整數,滿分為100分)進行統計,制成如下頻率分布表.
分數(分數段) | 頻數(人數) | 頻率 |
[60,70) | 9 | x |
[70,80) | y | 0.38 |
[80,90) | 16 | 0.32 |
[90,100) | z | s |
合計 | p | 1 |
(Ⅰ)求出上表中的x,y,z,s,p的值;
(Ⅱ)按規定,預賽成績不低于90分的選手參加決賽,參加決賽的選手按照抽簽方式決定出場順序.已知高一二班有甲、乙兩名同學取得決賽資格.
①求決賽出場的順序中,甲不在第一位、乙不在最后一位的概率;
②記高一二班在決賽中進入前三名的人數為X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列判斷錯誤的是
A. 若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ;
;
B. 若![]() 組數據
組數據![]() 的散點都在
的散點都在![]() 上,則相關系數
上,則相關系數![]() ;
;
C. 若隨機變量![]() 服從二項分布:
服從二項分布: ![]() , 則
, 則![]() ;
;
D. ![]() 是
是![]() 的充分不必要條件;
的充分不必要條件;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(0,﹣1)是拋物線C:x2=2py(p>0)準線上的一點,點F是拋物線C的焦點,點P在拋物線C上且滿足|PF|=m|PA|,當m取最小值時,點P恰好在以原點為中心,F為焦點的雙曲線上,則此雙曲線的離心率為( )
A.![]()
B.![]()
C.![]() +1
+1
D.![]() +1
+1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,滿足
,滿足![]() ,
,![]() .數列
.數列![]() 滿足
滿足![]() ,
,![]() ,且
,且![]() .
.
(1)求數列![]() 和
和![]() 的通項公式;
的通項公式;
(2)若![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,對任意的
,對任意的![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(3)是否存在正整數![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() (
(![]() )成等差數列,若存在,求出所有滿足條件的
)成等差數列,若存在,求出所有滿足條件的![]() ,
,![]() ,若不存在,請說明理由.
,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0),四點P1(1,1),P2(0,1),P3(–1,
(a>b>0),四點P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三點在橢圓C上.
)中恰有三點在橢圓C上.
(1)求C的方程;
(2)設直線l不經過P2點且與C相交于A,B兩點.若直線P2A與直線P2B的斜率的和為–1,證明:l過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,a,b,c分別是角A,B,C的對邊,且2cosAcosC(tanAtanC﹣1)=1.
(Ⅰ)求B的大小;
(Ⅱ)若 ![]() ,
, ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 滿足
滿足![]() .
.
(Ⅰ)當![]() 時,解不等式
時,解不等式![]() ;
;
(Ⅱ)若關于x的方程![]() 的解集中有且只有一個元素,求a的值;
的解集中有且只有一個元素,求a的值;
(Ⅲ)設![]() ,若對
,若對![]() ,函數
,函數![]() 在區間
在區間![]() 上的最大值與最小值的差不超過1,求a的取值范圍.
上的最大值與最小值的差不超過1,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com