
已知 是定義在R上的奇函數,當
是定義在R上的奇函數,當 時,
時, .
.
(1)求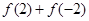 的值;
的值;
(2)求 的解析式;
的解析式;
(3)解關于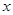 的不等式
的不等式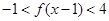 ,結果用集合或區間表示.
,結果用集合或區間表示.
(1)0
(2)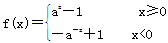
(3)當a>1時,不等式的解集為(1-loga2,1+loga5);當0<a<1時,不等式的解集為R.
解析試題分析:解 (1)∵f(x)是奇函數,∴f(-2)=-f(2),即f(2)+f(-2)=0.
(2)當x<0時,-x>0,∴f(-x)=a-x-1.
∵f(x)是奇函數,有f(-x)=-f(x),∴f(x)=-a-x+1(x<0).
∴所求的解析式為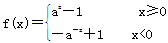 .
.
(3)不等式等價于 或
或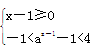 ,
,
即 或
或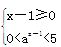 .
.
當a>1時,有 或
或 ,注意此時loga2>0,loga5>0,
,注意此時loga2>0,loga5>0,
可得此時不等式的解集為(1-loga2,1+loga5).
同理可得,當0<a<1時,不等式的解集為R.
綜上所述,當a>1時,不等式的解集為(1-loga2,1+loga5);當0<a<1時,不等式的解集為R.
考點:不等式的應用
點評:解決的關鍵是對于奇偶性和單調性的應用,屬于基礎題。


 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作業本系列答案
名校作業本系列答案科目:高中數學 來源:2012-2013學年四川省成都市武侯區玉林中學高一(上)期中數學試卷(解析版) 題型:填空題
查看答案和解析>>
科目:高中數學 來源:2012-2013學年福建省高三第一次階段考試理科數學試卷(解析版) 題型:解答題
(本小題滿分13分)已知 是定義在R上的奇函數,當
是定義在R上的奇函數,當 時
時 ;
;
(1)求函數 的表達式;
的表達式;
(2)畫出其大致圖像并指出其單調區間.
(3)若函數 -1有三個零點,求K的取值范圍;
-1有三個零點,求K的取值范圍;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com