
探究函數f(x)=x+ ,x∈(0,+∞)的最小值,并確定取得最小值時x的值.列表如下:
,x∈(0,+∞)的最小值,并確定取得最小值時x的值.列表如下:
|
x |
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
|
y |
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.02 |
4.04 |
4.3 |
5 |
5.8 |
7.57 |
… |
請觀察表中y值隨x值變化的特點,完成以下的問題.
函數f(x)=x+ (x>0)在區間(0,2)上遞減;
(x>0)在區間(0,2)上遞減;
(1)函數f(x)=x+ (x>0)在區間 上遞增.
(x>0)在區間 上遞增.
當x= 時,y最小= .
(2)證明:函數f(x)=x+ 在區間(0,2)上遞減.
在區間(0,2)上遞減.
(3)思考:函數f(x)=x+ (x<0)有最值嗎?如果有,那么它是最大值還是最小值?此時x為何值?(直接回答結果,不需證明)
(x<0)有最值嗎?如果有,那么它是最大值還是最小值?此時x為何值?(直接回答結果,不需證明)
(1)(2,+∞);2;4(2)證明如下(3)當x=-2時,有最大值-4
【解析】
試題分析:(1)(2,+∞);2;4
(2)任取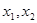 ∈(0, 2)且
∈(0, 2)且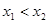 于是,f(
于是,f(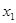 )-f(
)-f(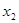 )
)
=(x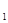 +
+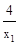 )-(x2+
)-(x2+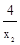 ) =
) =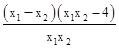
(1)∵ x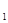 , x
, x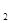 ∈(0, 2)
且 x
∈(0, 2)
且 x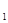 <x
<x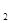
∴ x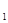 -x
-x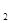 <0;x
<0;x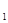 x
x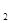 -4<0; x
-4<0; x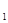 x
x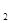 >0
>0
∴(1)式>0 即f(x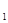 )-f(x
)-f(x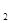 )>0,f(x
)>0,f(x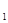 )>f(x
)>f(x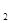 )
)
∴f(x)在區間(0, 2)遞減. 10分
(3)當x=-2時,有最大值-4提示:f(x)在(-∞,0)∪(0, ∞)
為奇函數.圖象關于原點對稱.
考點:函數的單調性;函數的最值
點評:證明函數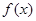 在區間
在區間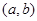 上為增(減)函數的方法是:令
上為增(減)函數的方法是:令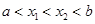 ,若
,若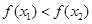
(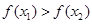 ),則函數為增(減)函數。
),則函數為增(減)函數。


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:
| 4 |
| x |
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 4 |
| x |
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 4 |
| x |
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
查看答案和解析>>
科目:高中數學 來源:徐州模擬 題型:解答題
| 2 |
| ||
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com