(本小題滿分14分)
已知函數
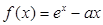
(
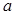
為常數)的圖像與
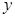
軸交于點
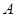
,曲線
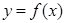
在點
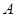
處的切線斜率為
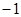
.
(1)求
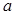
的值及函數
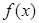
的極值;
(2)證明:當
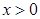
時,
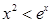
(3)證明:對任意給定的正數
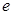
,總存在
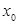
,使得當
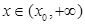
時,恒有
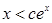
(1)當
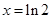
時,
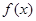
有極小值
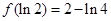
,
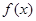
無極大值.
(2)見解析.(3)見解析.
試題分析:(1)由
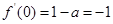
,得
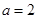
.
從而
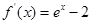
.
令
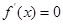
,得駐點
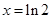
.討論可知:
當
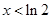
時,
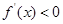
,
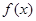
單調遞減;
當
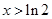
時,
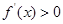
,
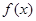
單調遞增.
當
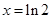
時,
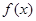
有極小值
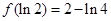
,
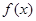
無極大值.
(2)令
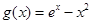
,則
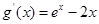
.
根據
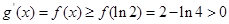
,知
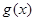
在R上單調遞增,又
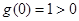
,
當
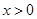
時,由
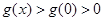
,即得.
(3)思路一:對任意給定的正數c,取
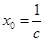
,
根據
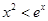
.得到當
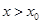
時,
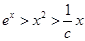
.
思路二:令
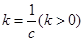
,轉化得到只需
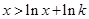
成立.
分
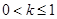
,
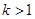
,應用導數研究
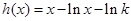
的單調性.
思路三:就①
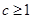
,②
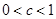
,加以討論.
試題解析:解法一:
(1)由
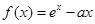
,得
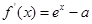
.
又
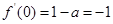
,得
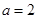
.
所以
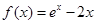
,
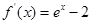
.
令
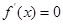
,得
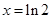
.
當
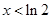
時,
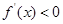
,
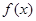
單調遞減;
當
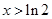
時,
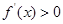
,
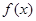
單調遞增.
所以當
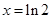
時,
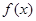
有極小值,
且極小值為
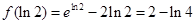
,
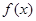
無極大值.
(2)令
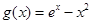
,則
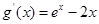
.
由(1)得,
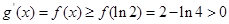
,即
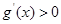
.
所以
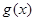
在R上單調遞增,又
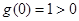
,
所以當
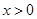
時,
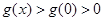
,即
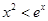
.
(3)對任意給定的正數c,取
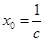
,
由(2)知,當
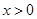
時,
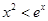
.
所以當
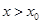
時,
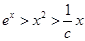
,即
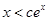
.
因此,對任意給定的正數c,總存在
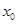
,當
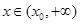
時,恒有
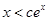
.
解法二:(1)同解法一.
(2)同解法一.
(3)令
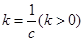
,要使不等式
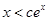
成立,只要
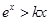
成立.
而要使
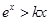
成立,則只需
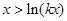
,即
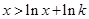
成立.
①若
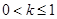
,則
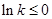
,易知當
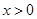
時,
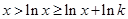
成立.
即對任意
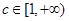
,取
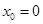
,當
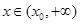
時,恒有
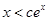
.
②若
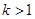
,令
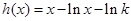
,則
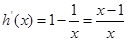
,
所以當
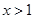
時,
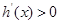
,
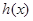
在
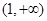
內單調遞增.
取
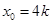
,
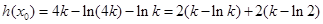
,
易知
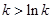
,
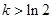
,所以
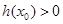
.
因此對任意
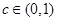
,取
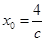
,當
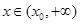
時,恒有
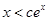
.
綜上,對任意給定的正數c,總存在
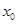
,當
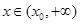
時,恒有
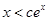
.
解法三:(1)同解法一.
(2)同解法一.
(3)①若
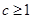
,取
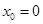
,
由(2)的證明過程知,
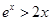
,
所以當
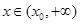
時,有
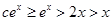
,即
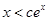
.
②若
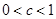
,
令
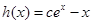
,則
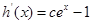
,
令
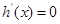
得
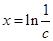
.
當
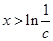
時,
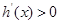
,
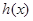
單調遞增.
取
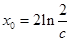
,
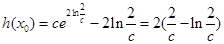
,
易知
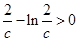
,又
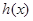
在
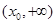
內單調遞增,
所以當
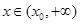
時,恒有
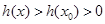
,即
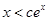
.
綜上,對任意給定的正數c,總存在
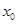
,當
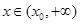
時,恒有
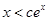
.
練習冊系列答案
相關習題
科目:高中數學
來源:不詳
題型:解答題
已知函數
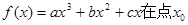
處取得極小值-4,使其導函數
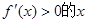
的取值范圍為(1,3)。
(1)求
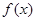
的解析式及
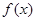
的極大值;
(2)當
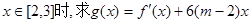
的最大值。
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知函數
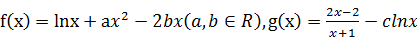
.
(1當
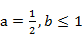
時,
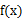
與
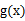
)在定義域上單調性相反,求的
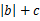
的最小值。
(2)當
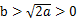
時,求證:存在
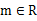
,使
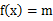
的三個不同的實數解
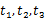
,且對任意
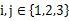
且
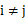
都有
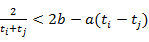
.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知常數

,函數
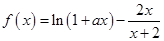
.
(1)討論
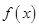
在區間

上的單調性;
(2)若
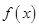
存在兩個極值點
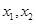
,且

,求
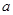
的取值范圍.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
定義在
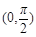
上的函數
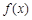
,
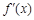
是它的導函數,且恒有
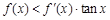
成立,則( )
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
已知

是二次函數,方程

有兩個相等的實數根,且

。
(1)求

的表達式;
(2)若直線

把

的圖象與兩坐標軸圍成的圖形面積二等分,求t的值.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:填空題
已知

在
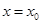
處取最大值。以下各式正確的序號為
.
①
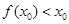
②
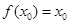
③
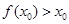
④
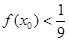
⑤
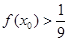
查看答案和解析>>
主站蜘蛛池模板:
国产精品久久久久久久久久久免费看
|
国产精品久久久久久婷婷天堂
|
欧日韩不卡在线视频
|
亚洲精品久久久久久久久久久
|
青草视频网站
|
日韩免费网站
|
91精品久久久久久久99
|
亚洲欧洲日韩
|
成人久久免费
|
免费视频99|
欧美一区视频
|
我和我的祖国电影在线观看免费版高清
|
青青草久久
|
欧美成人精品一区二区男人看
|
黄av在线免费观看
|
av天空
|
在线日韩欧美
|
国产高清在线精品一区
|
国产精品综合
|
久久免费精品视频
|
欧美亚洲国产精品
|
国产精品一区二区三区四区
|
久久精品久久精品国产大片
|
成人午夜精品一区二区三区
|
欧美一级免费
|
国产在线视频网
|
天天插天天射天天干
|
91免费在线|
黄色av电影
|
日韩一区电影
|
一级毛片观看
|
欧美www.|
免费v片|
亚洲一区二区三区四区五区中文
|
日韩视频在线观看
|
欧美午夜一区二区三区免费大片
|
国产欧美日本
|
狠狠综合
|
精品视频一区二区
|
日韩中文字幕在线视频
|
亚洲视频免费在线
|

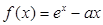 (
(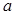 為常數)的圖像與
為常數)的圖像與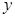 軸交于點
軸交于點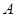 ,曲線
,曲線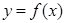 在點
在點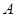 處的切線斜率為
處的切線斜率為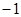 .
.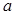 的值及函數
的值及函數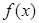 的極值;
的極值;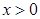 時,
時,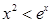
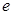 ,總存在
,總存在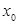 ,使得當
,使得當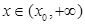 時,恒有
時,恒有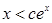
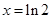 時,
時,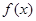 有極小值
有極小值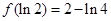 ,
,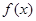 無極大值.
無極大值.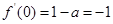 ,得
,得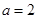 .
.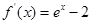 .
.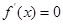 ,得駐點
,得駐點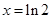 .討論可知:
.討論可知: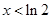 時,
時,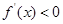 ,
,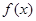 單調遞減;
單調遞減;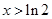 時,
時,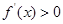 ,
,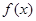 單調遞增.
單調遞增.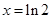 時,
時,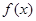 有極小值
有極小值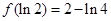 ,
,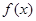 無極大值.
無極大值.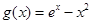 ,則
,則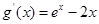 .
.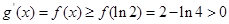 ,知
,知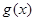 在R上單調遞增,又
在R上單調遞增,又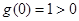 ,
,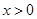 時,由
時,由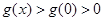 ,即得.
,即得.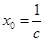 ,
,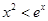 .得到當
.得到當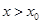 時,
時,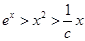 .
.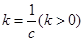 ,轉化得到只需
,轉化得到只需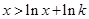 成立.
成立.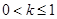 ,
,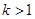 ,應用導數研究
,應用導數研究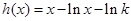 的單調性.
的單調性.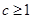 ,②
,②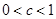 ,加以討論.
,加以討論.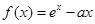 ,得
,得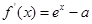 .
.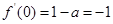 ,得
,得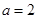 .
.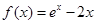 ,
,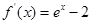 .
.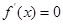 ,得
,得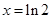 .
.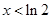 時,
時,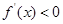 ,
,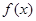 單調遞減;
單調遞減;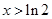 時,
時,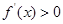 ,
,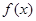 單調遞增.
單調遞增.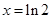 時,
時,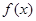 有極小值,
有極小值,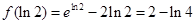 ,
,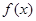 無極大值.
無極大值.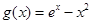 ,則
,則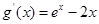 .
.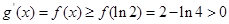 ,即
,即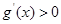 .
.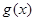 在R上單調遞增,又
在R上單調遞增,又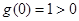 ,
,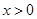 時,
時,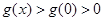 ,即
,即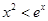 .
.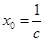 ,
,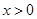 時,
時,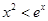 .
.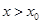 時,
時,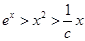 ,即
,即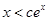 .
.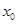 ,當
,當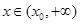 時,恒有
時,恒有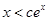 .
.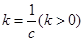 ,要使不等式
,要使不等式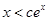 成立,只要
成立,只要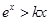 成立.
成立.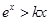 成立,則只需
成立,則只需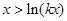 ,即
,即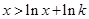 成立.
成立.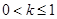 ,則
,則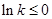 ,易知當
,易知當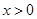 時,
時,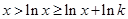 成立.
成立.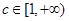 ,取
,取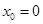 ,當
,當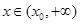 時,恒有
時,恒有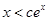 .
.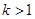 ,令
,令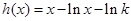 ,則
,則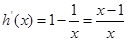 ,
,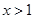 時,
時,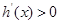 ,
,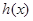 在
在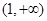 內單調遞增.
內單調遞增.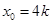 ,
,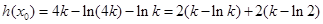 ,
,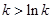 ,
,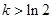 ,所以
,所以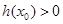 .
.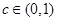 ,取
,取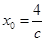 ,當
,當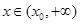 時,恒有
時,恒有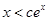 .
.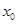 ,當
,當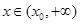 時,恒有
時,恒有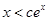 .
.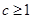 ,取
,取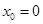 ,
,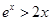 ,
,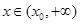 時,有
時,有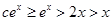 ,即
,即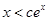 .
.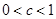 ,
,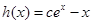 ,則
,則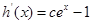 ,
,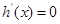 得
得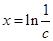 .
.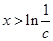 時,
時,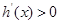 ,
,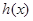 單調遞增.
單調遞增.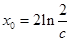 ,
,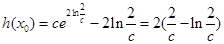 ,
,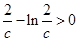 ,又
,又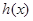 在
在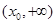 內單調遞增,
內單調遞增,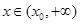 時,恒有
時,恒有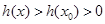 ,即
,即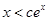 .
.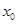 ,當
,當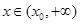 時,恒有
時,恒有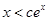 .
.

 備戰中考寒假系列答案
備戰中考寒假系列答案