【題目】已知甲、乙兩名工人在同樣條件下每天各生產100件產品，且每生產1件正品可獲利20元，生產1件次品損失30元，甲、乙兩名工人100天中出現次品件數的情況如表所示.
甲每天生產的次品數/件 | 0 | 1 | 2 | 3 | 4 |
對應的天數/天 | 40 | 20 | 20 | 10 | 10 |
乙每天生產的次品數/件 | 0 | 1 | 2 | 3 |
對應的天數/天 | 30 | 25 | 25 | 20 |
（1）將甲每天生產的次品數記為
（單位：件），日利潤記為
（單位：元），寫出與的函數關系式；
（2）按這100天統計的數據，分別求甲、乙兩名工人的平均日利潤.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】給出下列命題：
①線性相關系數
越大，兩個變量的線性相關性越強；反之，線性相關性越弱；
②用
來刻畫回歸效果，越大，說明模型的擬合效果越好；
③根據
列聯表中的數據計算得出的
的值越大，兩類變量相關的可能性就越大；
④在回歸分析模型中，殘差平方和越小，說明模型的擬合效果越好；
⑤從勻速傳遞的產品生產流水線上，質檢員每10分鐘從中抽取一件產品進行某項指標檢測，這樣的抽樣是分層抽樣．
其中真命題的序號是_______．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，邊長為
的正方形
和高為
的等腰梯形
所在的平面互相垂直，
，
，
與
交于點
，點
為線段
上任意一點.
（Ⅰ）求證：
平面
；
（Ⅱ）求
與平面所成角的正弦值；
（Ⅲ）是否存在點使平面
與平面垂直，若存在，求出
的值，若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業新研發了一種產品，產品的成本由原料成本及非原料成本組成，每件產品的非原料成本y（元）與生產該產品的數量x（千件）有關，經統計得到如下數據：
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y | 112 | 61 | 44.5 | 35 | 30.5 | 28 | 25 | 24 |
根據以上數據，繪制了散點圖．
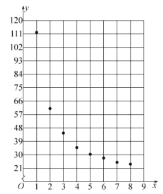
參考數據：（其中
）
|
|
|
|
|
|
183.4 | 0.34 | 0.115 | 1.53 | 360 | 22385.8 |
參考公式：對于一組數據
，
，其回歸直線
的斜率和截距的最小二乘估計分別為：
．
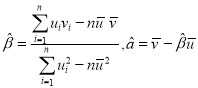（1）觀察散點圖判斷，
與
哪一個適宜作為非原料成本y與生產該產品的數量x的回歸方程類型？（給出判斷即可，不必說明理由）
（2）根據（1）的判斷結果及表中數據，建立y與x的回歸方程．
（3）試預測生產該產品10000件時每件產品的非原料成本.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是某電視臺主辦的歌手大獎賽上七位評委為甲、乙兩名選手打出的分數的莖葉圖（其中
為數字0~9中的一個），則下列結論中正確的是（ ）
A. 甲選手的平均分有可能和乙選手的平均分相等
B. 甲選手的平均分有可能比乙選手的平均分高
C. 甲選手所有得分的中位數比乙選手所有得分的中位數低
D. 甲選手所有得分的眾數比乙選手所有得分的眾數高
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某工廠為提高生產效率，開展技術創新活動，提出了完成某項生產任務的兩種新的生產方式．為比較兩種生產方式的效率，選取40名工人，將他們隨機分成兩組，每組20人，第一組工人用第一種生產方式，第二組工人用第二種生產方式．根據工人完成生產任務的工作時間（單位：min）繪制了如下莖葉圖：
（1）根據莖葉圖判斷哪種生產方式的效率更高？并說明理由；
（2）求40名工人完成生產任務所需時間的中位數
，并將完成生產任務所需時間超過和不超過的工人數填入下面的列聯表：
超過 | 不超過 | |
第一種生產方式 | ||
第二種生產方式 |
（3）根據（2）中的列聯表，能否有99%的把握認為兩種生產方式的效率有差異？
附：
，
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某年級組織學生參加了某項學術能力測試,為了解參加測試學生的成績情況,從中隨機抽取20名學生的測試成績作為樣本,規定成績大于或等于80分的為優秀,否則為不優秀.統計結果如圖:
(1)求
的值和樣本的平均數;
(2)從該樣本成績優秀的學生中任選兩名,求這兩名學生的成績至少有一個落在
內的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】部分與整體以某種相似的方式呈現稱為分形.謝爾賓斯基三角形是一種分形，由波蘭數學家謝爾賓斯基1915年提出.具體操作是取一個實心三角形，沿三角形的三邊中點連線，將它分成4個小三角形，去掉中間的那一個小三角形后，對其余3個小三角形重復上述過程逐次得到各個圖形，如圖.
現在上述圖(3)中隨機選取一個點，則此點取自陰影部分的概率為_________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
