已知曲線y=2x-x3上一點P(-1,-1),求:
(1)點P處的切線方程;
(2)點P處的切線與x軸、y軸所圍成的平面圖形的面積.
【答案】
分析:(1)正確求解函數的導函數是解決本題的關鍵,把握好函數在點P處的切線的斜率與導數之間的關系,注意點斜式方程的準確運用;
(2)求出該切線與x軸、y軸的交點坐標是解決本題的關鍵,運用所得圖形是直角三角形,根據直角三角形的面積計算公式求出所得圖形的面積.
解答:解:(1)y'=2-3x
2∴y'|
x=-1=2-3×(-1)
2=-1,
∴切線方程為y-(-1)=-[x-(-1)]
即x+y+2=0
(2)切線x+y+2=0在x軸、y軸上的截距都是-2,
故切線與x軸、y軸所圍成的平面圖形為直角三角形,
其面積為
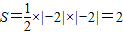
.
點評:本題考查函數的導數的幾何意義,考查學生運用基本的導數知識解決數學問題的能力和方法,考查學生的運算能力、轉化與化歸的思想和方法.注意直線與坐標軸圍成圖形的面積的求法.

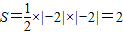 .
.

 閱讀快車系列答案
閱讀快車系列答案