
【題目】已知函數f(x)=(x﹣a)cosx﹣sinx,g(x)![]() x3
x3![]() ax2,a∈R
ax2,a∈R
(1)當a=1時,求函數y=f(x)在區間(0,![]() )上零點的個數;
)上零點的個數;
(2)令F(x)=f(x)+g(x),試討論函數y=F(x)極值點的個數.
【答案】(1)零點的個數為0,(2)無極值.
【解析】
(1)結合函數![]() 的單調性和極值,即可得到本題答案;
的單調性和極值,即可得到本題答案;
(2)先求導,再分類討論,即可得到![]() 的單調區間和極值,由此即可得到本題答案.
的單調區間和極值,由此即可得到本題答案.
(1)當![]() 時,
時,![]() ,
,
∴![]() ,
,
因為當![]() 時,
時,![]() ,
,
所以當![]() 時,
時,![]() ,
,![]() 單調遞增,當
單調遞增,當![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
當![]() 時,函數取得最大值
時,函數取得最大值![]() ,
,
所以函數![]() 在區間
在區間![]() 上零點的個數為0;
上零點的個數為0;
(2)![]() ,
,
![]() ,
,
令![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上為增函數,又
上為增函數,又![]() ,
,
所以當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() .
.
①若![]() 時,
時,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞減,
上單調遞減,
故有2個極值;
②若![]() 時,
時,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞減,
上單調遞減,
故有2個極值點;
③當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() 恒成立,故
恒成立,故![]() 在
在![]() 上單調遞增,
上單調遞增,
∴![]() 在R上單調遞增,無極值點.
在R上單調遞增,無極值點.


科目:高中數學 來源: 題型:
【題目】某企業生產的某種產品被檢測出其中一項質量指標存在問題.該企業為了檢查生產該產品的甲、乙兩條流水線的生產情況,隨機地從這兩條流水線上生產的大量產品中各抽取50件產品作為樣本,測出它們的這一項質量指標值.若該項質量指標值落在![]() 內,則為合格品,否則為不合格品.如圖是甲流水線樣本的頻數分布表和乙流水線樣本的頻率分布直方圖.
內,則為合格品,否則為不合格品.如圖是甲流水線樣本的頻數分布表和乙流水線樣本的頻率分布直方圖.
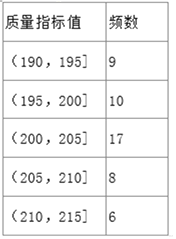
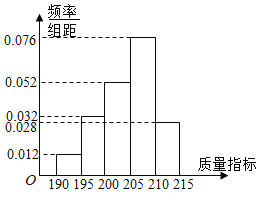
(1)根據頻率分布直方圖,估計乙流水線生產的產品該質量指標值的中位數;
(2)若將頻率視為概率,某個月內甲、乙兩條流水線均生產了5000件產品,則甲、乙兩條流水線分別生產出不合格品約多少件?
(3)根據已知條件完成下面![]() 列聯表,并回答是否有
列聯表,并回答是否有![]() 的把握認為“該企業生產的這種產品的質量指標值與甲、乙兩條流水線的選擇有關”?
的把握認為“該企業生產的這種產品的質量指標值與甲、乙兩條流水線的選擇有關”?
甲流水線 | 乙流水線 | 合計 | |
合格品 | |||
不合格品 | |||
合計 |
附:![]() ,其中
,其中![]() .
.
臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,其中
,其中![]() .
.
(1)求過點![]() 和函數
和函數![]() 的圖像相切的直線方程;
的圖像相切的直線方程;
(2)若對任意![]() ,有
,有![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)若存在唯一的整數![]() ,使得
,使得![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】把函數![]() 的圖象向右平移一個單位,所得圖象與函數
的圖象向右平移一個單位,所得圖象與函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱;已知偶函數
對稱;已知偶函數![]() 滿足
滿足![]() ,當
,當![]() 時,
時,![]() ;若函數
;若函數![]() 有五個零點,則
有五個零點,則![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為側棱
為側棱![]() 上一點.
上一點.

(1)若![]() ,求證:
,求證:![]()
![]() 平面
平面![]() ;
;
(2)求證:平面![]() 平面
平面![]() ;
;
(3)在側棱![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ? 若存在,求出線段
? 若存在,求出線段![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在![]() 中,
中, ![]() ,
, ![]() 分別為
分別為![]() ,
, ![]() 的中點,
的中點,![]() 為
為![]() 的中點,
的中點,![]() ,
,![]() .將
.將![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,如圖2.
,如圖2.
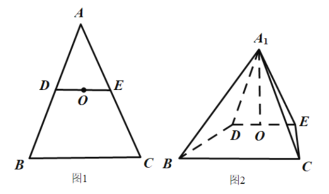
(1)求證:![]() ;
;
(2)求直線![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市有![]() 兩家大型石油煉化廠,這兩家石油煉化廠所生產的成品油都要通過甲、乙兩條輸油管道輸送到各地進行銷售.由于地理位置及
兩家大型石油煉化廠,這兩家石油煉化廠所生產的成品油都要通過甲、乙兩條輸油管道輸送到各地進行銷售.由于地理位置及![]() 兩家石油煉化廠的生產能力的不同,
兩家石油煉化廠的生產能力的不同,![]() 石油煉化廠生產的成品油通過甲、乙兩條輸油管道輸送時每噸的運費分別為1元和1.6元,
石油煉化廠生產的成品油通過甲、乙兩條輸油管道輸送時每噸的運費分別為1元和1.6元,![]() 石油煉化廠生產的成品油通過甲、乙兩條輸油管道輸送時每噸的運費分別為0.8元和1.5元.甲輸油管道每年最多能輸送290萬噸成品油,乙輸油管道每年最多能輸送320萬噸成品油.
石油煉化廠生產的成品油通過甲、乙兩條輸油管道輸送時每噸的運費分別為0.8元和1.5元.甲輸油管道每年最多能輸送290萬噸成品油,乙輸油管道每年最多能輸送320萬噸成品油.![]() 石油煉化廠每年生產180萬噸成品油,
石油煉化廠每年生產180萬噸成品油,![]() 石油煉化廠每年生產240萬噸成品油.規定
石油煉化廠每年生產240萬噸成品油.規定![]() 石油煉化廠通過甲輸油管道輸送的成品油與
石油煉化廠通過甲輸油管道輸送的成品油與![]() 石油煉化廠通過甲輸油管道輸送的成品油的二倍之和不超過490萬噸.問:兩家煉化廠采用什么樣的輸油方案,能使總的運費最少?
石油煉化廠通過甲輸油管道輸送的成品油的二倍之和不超過490萬噸.問:兩家煉化廠采用什么樣的輸油方案,能使總的運費最少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,
,![]() ,上頂點為B,右焦點為F,已知直線
,上頂點為B,右焦點為F,已知直線![]() 的傾斜角為120°,
的傾斜角為120°,![]() .
.
(1)求橢圓C的方程;
(2)設P為橢圓C上不同于![]() ,
,![]() 的一點,O為坐標原點,線段
的一點,O為坐標原點,線段![]() 的垂直平分線交
的垂直平分線交![]() 于M點,過M且垂直于
于M點,過M且垂直于![]() 的直線交y軸于Q點,若
的直線交y軸于Q點,若![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】幾位大學生響應國家的創業號召,開發了一款應用軟件.為激發大家學習數學的興趣,他們推出了“解數學題獲取軟件激活碼”的活動.這款軟件的激活碼為下面數學問題的答案:已知數列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一項是20,接下來的兩項是20,21,再接下來的三項是20,21,22,依此類推.求滿足如下條件的最小整數N:N>100且該數列的前N項和為2的整數冪.那么該款軟件的激活碼是
A. 440B. 330
C. 220D. 110
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com