
【題目】已知![]() .
.
(1)對一切![]() ,
, ![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,求函數
時,求函數![]() 在[m,m+3]( m>0)上的最值;
在[m,m+3]( m>0)上的最值;
(3)證明:對一切![]() ,都有
,都有![]() 成立.
成立.
【答案】(1)![]()
![]() (2)見解析
(2)見解析
【解析】
試題分析:(1)根據對一切![]() 恒成立,也就是
恒成立,也就是![]() 在
在![]() 恒成立,下面只要求出函數的最小值,使得
恒成立,下面只要求出函數的最小值,使得![]() 小于函數的最小值即可;(2)要求函數最值,不管遇到什么特殊的函數,一定要按照求最值的方法按部就班的來解,首先求導,令導函數對于零,得到可能是極值點,根據極值點和區間兩個端點之間的關系,得到結果;(3)要證不等式在一個區間上恒成立,把問題進行等價變形,由(2)知
小于函數的最小值即可;(2)要求函數最值,不管遇到什么特殊的函數,一定要按照求最值的方法按部就班的來解,首先求導,令導函數對于零,得到可能是極值點,根據極值點和區間兩個端點之間的關系,得到結果;(3)要證不等式在一個區間上恒成立,把問題進行等價變形,由(2)知![]() 時,
時, ![]() 的最小值是
的最小值是![]() ,只要求函數
,只要求函數![]() 最大值進行比較即可.
最大值進行比較即可.
試題解析:(1)對一切![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
也就是![]()
![]() 在
在![]() 恒成立. 令
恒成立. 令![]() ,
,
則![]()
![]() ,
,
在![]() 上
上![]()
![]() ,在
,在![]() 上
上![]()
![]() ,
,
因此,![]() 在
在![]() 處取極小值,也是最小值,即
處取極小值,也是最小值,即![]() ,所以
,所以![]() .
.
(2)當![]()
![]() ,
,![]()
![]() ,由
,由![]()
![]() 得
得![]() .
.
①當![]() 時,在
時,在![]() 上
上![]()
![]() ,在
,在![]() 上
上![]()
![]()
因此,![]() 在
在![]() 處取得極小值,也是最小值.
處取得極小值,也是最小值. ![]() .
.
由于![]()
因此,![]() .
.
②當![]() ,
,![]() ,因此
,因此![]() 上單調遞增,所以
上單調遞增,所以![]() ,
,![]() .
.
(3)證明:問題等價于證明![]() ,
,
由(Ⅱ)知![]() 時,
時,![]() 的最小值是
的最小值是![]() ,當且僅當
,當且僅當![]() 時取得,
時取得,
設![]() ,則
,則![]()
![]() ,易知
,易知
![]() ,當且僅當
,當且僅當![]() 時取到,
時取到,
但![]() 從而可知對一切
從而可知對一切![]() ,都有
,都有![]() 成立.
成立.


科目:高中數學 來源: 題型:
【題目】某工廠今年1月、2月、3月生產某種產品的數量分別是1萬件、2萬件、1.3萬件,為了預測以后每個月的產量,以這三個月的產品數量為依據,用一個函數模擬該產品的月產量y與月份x的關系,模擬函數可以選用二次函數或函數y=abx+c(其中a,b,c為常數),已知4月份該產品的產量為1.37萬件,請問用以上哪個函數作為模擬函數較好?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電動小汽車生產企業,年利潤![]() (出廠價
(出廠價![]() 投入成本)
投入成本)![]() 年銷售量.已知上年度生產電動小汽車的投入成本為
年銷售量.已知上年度生產電動小汽車的投入成本為![]() 萬元/輛,出廠價為
萬元/輛,出廠價為![]() 萬/輛,年銷售量為
萬/輛,年銷售量為![]() 輛,本年度為打造綠色環保電動小汽車,提高產品檔次,計劃增加投入成本,若每輛電動小汽車投入成本增加的比例為
輛,本年度為打造綠色環保電動小汽車,提高產品檔次,計劃增加投入成本,若每輛電動小汽車投入成本增加的比例為![]() (
(![]() ),則出廠價相應提高的比例為
),則出廠價相應提高的比例為![]() .同時年銷售量增加的比例為
.同時年銷售量增加的比例為![]() .
.
(1)寫出本年度預計的年利潤![]() (萬元)與投入成本增加的比例
(萬元)與投入成本增加的比例![]() 的函數關系式;
的函數關系式;
(2)為了使本年度的年利潤最大,每輛車投入成本增加的比例應為多少?最大年利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
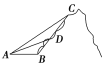
【題目】如圖,嵩山上原有一條筆直的山路BC,現在又新架設了一條索道AC,小李在山腳B處看索道AC,發現張角∠ABC=120°;從B處攀登400米到達D處,回頭看索道AC,發現張角∠ADC=150°;從D處再攀登800米方到達C處,則索道AC的長為________米.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點
的右焦點![]() ,橢圓
,橢圓![]() 的左,右頂點分別為
的左,右頂點分別為![]() .過點
.過點![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點,且
兩點,且![]() 的面積是
的面積是![]() 的面積的3倍.
的面積的3倍.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若![]() 與
與![]() 軸垂直,
軸垂直,![]() 是橢圓
是橢圓![]() 上位于直線
上位于直線![]() 兩側的動點,且滿足
兩側的動點,且滿足![]() ,試問直線
,試問直線![]() 的斜率是否為定值,請說明理由.
的斜率是否為定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某批零件共160個,其中一級品有48人,二級品有64個,三級品有32個,等外品有16個.從中抽取一個容量為20的樣本.試簡要敘述用簡單隨機抽樣、系統抽樣、分層抽樣法進行抽樣都是等可能抽樣.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com