【題目】設集合
，
，映射
,使得
，已知
，
.則x,y,u的值分別是____.
【答案】1，9，8，6
【解析】
由題意知uv-xy=39，uy-xv=66，u、v、x、y都是非負整數且不超過11.
則有(y+v)(u-x)=105，(y-v)(u+x)=27.又0≤y≤11，0≤v≤11.
所以，
，即
.從而5≤u-x≤10，于是u+x≥5.
又(y-v)(u+x)=1×27=3×9=9×3，則u+x=9或27.
而0≤u+x≤22，因此，u+x=9.
由u+x=9得y-v=3.
由(y+v)(u-x)=10×5=3×35=5×21=15×7=21×5得y+v=15或21.
當y+v=15時，u-x=7，得y=9，v=6，u=8，x=1；
當y+v=21時，u-x=5，則u=7，x=2，y=12，v=9但0≤y≤11，則此結果不合題意.
故所求x、y、u、v的值分別為x=1，y=9，u=8，v=6.
優生樂園系列答案科目：高中數學 來源： 題型：
【題目】給定兩個七棱錐，它們有公共面的底面
，頂點
、
在底面的兩則.現將下述線段中的每一條染紅、藍兩色之一:
，底面上的所有對角線和所有的側棱.求證：圖中心存在一個同色三角形.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知Sn為數列{an}的前n項和，且Sn+2＝2an，n∈N*.
（1）求數列{an}的通項公式；
（2）令bn
，設數列{bn}的前項和為Tn，若Tn
，求n的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】去年，相關部門對某城市“五朵金花”之一的某景區在“十一”黃金周中每天的游客人數作了統計，其頻率分布如下表所示：
時間 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
頻率 | 0.05 | 0.08 | 0.09 | 0.13 | 0.30 | 0.15 | 0.20 |
已知10月1日這天該景區的營業額約為8萬元，假定這七天每天游客人均消費相同，則這個黃金周該景區游客人數最多的那一天的營業額約為______萬元.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知下列命題：
①在線性回歸模型中，相關指數
越接近于1，表示回歸效果越好；
②兩個變量相關性越強，則相關系數r就越接近于1；
③在回歸直線方程
中，當解釋變量
每增加一個單位時，預報變量
平均減少0.5個單位；
④兩個模型中殘差平方和越小的模型擬合的效果越好.
⑤回歸直線
恒過樣本點的中心
，且至少過一個樣本點；
⑥若
的觀測值滿足≥6.635，我們有99%的把握認為吸煙與患肺病有關系，那么在100個吸煙的人中必有99人患有肺病；
⑦從統計量中得知有95%的把握認為吸煙與患肺病有關系，是指有5%的可能性使得推斷出現錯誤． 其中正確命題的序號是__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】共享單車的投放，方便了市民短途出行，被譽為中國“新四大發明”之一.某市為研究單車用戶與年齡的相關程度，隨機調查了100位成人市民，統計數據如下：
不小于40歲 | 小于40歲 | 合計 | |
單車用戶 | 12 | y | m |
非單車用戶 | x | 32 | 70 |
合計 | n | 50 | 100 |
（1）求出列聯表中字母x、y、m、n的值；
（2）①從此樣本中，對單車用戶按年齡采取分層抽樣的方法抽出5人進行深入調研，其中不小于40歲的人應抽多少人？
②從獨立性檢驗角度分析，能否有
以上的把握認為該市成人市民是否為單車用戶與年齡是否小于40歲有關.
下面臨界值表供參考：
P（ | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，某景區內有兩條道路
、
，現計劃在上選擇一點
，新建道路
，并把
所在的區域改造成綠化區域.已知
，
，
.若綠化區域改造成本為
萬元
，新建道路成本為萬元
.
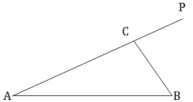
（1）①設
，寫出該計劃所需總費用
的表達式，并寫出
的范圍；
②設
，寫出該計劃所需總費用
的表達式，并寫出
的范圍；
（2）從上面兩個函數關系中任選一個，求點在何處時改造計劃的總費用最小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
