Question

若關于x的方程2^2x+2^x•a+a+1=0有實根，試求a的取值范圍．

Answer 1

解：令2^x=t＞0，原方程即為t²+at+a+1=0
則原方程有實根等價于關于t的方程t²+at+a+1=0至少有一正根．
于是有a+1＜0或a+1=0或
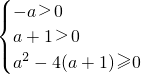
解得a．
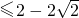
故實數a的取值范圍是（-∞，2-2]．
分析：先令t=2^x，則關于t方程為t²+at+a+1=0 有實根，結合二次方程根的分布即可解出實數a的取值范圍．
點評：本題主要考查了函數的零點與方程根的關系，以及利用二次方程根的分布求變量范圍，屬于中檔題．