
 =
=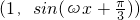 ,
, =
=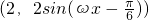 (其中ω為正常數)
(其中ω為正常數)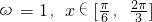 ,求
,求 ∥
∥ 時tanx的值;
時tanx的值; •
• -2,若函數f(x)的圖象的相鄰兩個對稱中心的距離為
-2,若函數f(x)的圖象的相鄰兩個對稱中心的距離為 ,求f(x)在區間
,求f(x)在區間 上的最小值.
上的最小值. ∥
∥ 時,
時, ,(2分)
,(2分)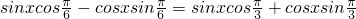
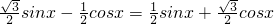 (4分)
(4分)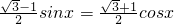 ,
,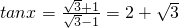 (6分)
(6分) =
=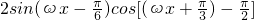 =
=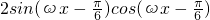 =
=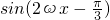 .(9分)
.(9分) =
= =
=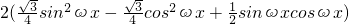 =
= (9分)
(9分)
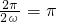 ,解之,得ω=1.(11分)
,解之,得ω=1.(11分) .
. ,所以
,所以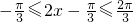 .
.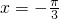 時,f(x)取最小值
時,f(x)取最小值 (14分)
(14分)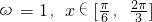 ,利用
,利用 ∥
∥ ,推出
,推出 ,然后利用兩角差與和的正弦函數,化簡求出tanx的值;
,然后利用兩角差與和的正弦函數,化簡求出tanx的值; •
• -2,根據函數f(x)的圖象的相鄰兩個對稱中心的距離為
-2,根據函數f(x)的圖象的相鄰兩個對稱中心的距離為 ,確定周期求出ω,然后求f(x)在區間
,確定周期求出ω,然后求f(x)在區間 上的最小值.
上的最小值.

 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com