
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求曲線![]() 的直角坐標方程,并說明它為何種曲線;
的直角坐標方程,并說明它為何種曲線;
(Ⅱ)設點![]() 的坐標為
的坐標為![]() ,直線
,直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】已知在正三棱柱![]() 中,側棱長
中,側棱長![]() 為3,H、G分別是AB,
為3,H、G分別是AB,![]() 中點.
中點.
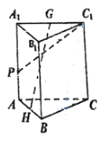
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() ,求此三棱柱的側面積;
,求此三棱柱的側面積;
(3)若P為側棱![]() 上一點,且
上一點,且![]() ,
,![]() 與平面
與平面![]() 所成角大小為
所成角大小為![]() ,求此三棱柱的體積.
,求此三棱柱的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年我國全面建成小康社會,其中小康生活的住房標準是城鎮人均住房建筑面積30平方米. 下表為2007年—2016年中,我區城鎮和農村人均住房建筑面積統計數據. 單位:平方米.
2007年 | 2008年 | 2009年 | 2010年 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | |
城鎮 | 18.66 | 20.25 | 22.79 | 25 | 27.1 | 28.3 | 31.6 | 32.9 | 34.6 | 36.6 |
農村 | 23.3 | 24.8 | 26.5 | 27.9 | 30.7 | 32.4 | 34.1 | 37.1 | 41.4 | 45.8 |
(1)現從上述表格中隨機抽取一年數據,試估計該年城鎮人均住房建筑面積達到小康生活住房標準的概率;
(2)現從上述表格中隨機抽取連續兩年數據,求這兩年中城鎮人均住房建筑面積增長不少于2平方米的概率;
(3)將城鎮和農村的人均住房建筑面積經四舍五入取整后作為樣本數據.記2012—2016年中城鎮人均住房面積的方差為![]() ,農村人均住房面積的方差為
,農村人均住房面積的方差為![]() ,判斷
,判斷![]() 與
與![]() 的大小.(只需寫出結論).
的大小.(只需寫出結論).
(注:方差![]() ,其中
,其中![]() 為
為 ![]()
![]() ,……
,…… ![]() 的平均數)
的平均數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某興趣小組在科學館的帕斯卡三角儀器前進行探究實驗.如圖所示,每次使一個實心小球從帕斯卡三角儀器的頂部入口落下,當它在依次碰到每層的菱形擋板時,會等可能地向左或者向右落下,在最底層的7個出口處各放置一個容器接住小球,該小組連續進行200次試驗,并統計容器中的小球個數得到柱狀圖:
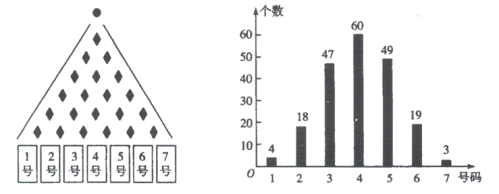
(Ⅰ)用該實驗來估測小球落入4號容器的概率,若估測結果的誤差小于![]() ,則稱該實驗是成功的.試問:該興趣小組進行的實驗是否成功?(誤差
,則稱該實驗是成功的.試問:該興趣小組進行的實驗是否成功?(誤差![]() )
)
(Ⅱ)再取3個小球進行試驗,設其中落入4號容器的小球個數為![]() ,求
,求![]() 的分布列與數學期望.(計算時采用概率的理論值)
的分布列與數學期望.(計算時采用概率的理論值)
查看答案和解析>>
科目:高中數學 來源: 題型:
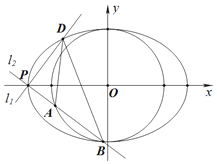
【題目】如圖,已知![]() 是橢圓
是橢圓![]() 的一個頂點,
的一個頂點,![]() 的短軸是圓
的短軸是圓![]() 的直徑,直線
的直徑,直線![]() ,
,![]() 過點P且互相垂直,
過點P且互相垂直,![]() 交橢圓
交橢圓![]() 于另一點D,
于另一點D,![]() 交圓
交圓![]() 于A,B兩點
于A,B兩點
![]() Ⅰ
Ⅰ![]() 求橢圓
求橢圓![]() 的標準方程;
的標準方程;
![]() Ⅱ
Ⅱ![]() 求
求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】央視傳媒為了解央視舉辦的“朗讀者”節目的收視時間情況,隨機抽取了某市名![]() 觀眾進行調查,其中有
觀眾進行調查,其中有![]() 名男觀眾和
名男觀眾和![]() 名女觀眾,將這
名女觀眾,將這![]() 名觀眾收視時間編成如圖所示的莖葉圖(單位:分鐘),收視時間在
名觀眾收視時間編成如圖所示的莖葉圖(單位:分鐘),收視時間在![]() 分鐘以上(包括
分鐘以上(包括![]() 分鐘)的稱為“朗讀愛好者”,收視時間在
分鐘)的稱為“朗讀愛好者”,收視時間在![]() 分鐘以下(不包括
分鐘以下(不包括![]() 分鐘)的稱為“非朗讀愛好者”.
分鐘)的稱為“非朗讀愛好者”.

(1)若采用分層抽樣的方法從“朗讀愛好者”和“非朗讀愛好者”中隨機抽取![]() 名,再從這
名,再從這![]() 名觀眾中任選
名觀眾中任選![]() 名,求至少選到
名,求至少選到![]() 名“朗讀愛好者”的概率;
名“朗讀愛好者”的概率;
(2)若從收視時間在40分鐘以上(包括40分鐘)的所有觀眾中選出男、女觀眾各1名,求選出的這兩名觀眾時間相差5分鐘以上的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某老師是省級課題組的成員,主要研究課堂教學目標達成度,為方便研究,從實驗班中隨機抽取30次的隨堂測試成績進行數據分析![]() 已知學生甲的30次隨堂測試成績如下
已知學生甲的30次隨堂測試成績如下![]() 滿分為100分
滿分為100分![]() :
:

![]() 把學生甲的成績按
把學生甲的成績按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6組,列出頻率分布表,并畫出頻率分布直方圖;
分成6組,列出頻率分布表,并畫出頻率分布直方圖;
![]() 規定隨堂測試成績80分以上
規定隨堂測試成績80分以上![]() 含80分
含80分![]() 為優秀,為幫助學生甲提高成績,選取學生乙,對甲與乙的隨堂測試成績進行對比分析,甲與乙測試成績是否為優秀相互獨立
為優秀,為幫助學生甲提高成績,選取學生乙,對甲與乙的隨堂測試成績進行對比分析,甲與乙測試成績是否為優秀相互獨立![]() 已知甲成績優秀的概率為
已知甲成績優秀的概率為![]() 以頻率估計概率
以頻率估計概率![]() ,乙成績優秀的概率為
,乙成績優秀的概率為![]() ,若
,若![]() ,則此二人適合為學習上互幫互助的“對子”
,則此二人適合為學習上互幫互助的“對子”![]() 在一次隨堂測試中,記
在一次隨堂測試中,記![]() 為兩人中獲得優秀的人數,已知
為兩人中獲得優秀的人數,已知![]() ,問二人是否適合結為“對子”?
,問二人是否適合結為“對子”?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com