
已知數列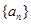 前
前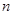 項和
項和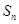 滿足
滿足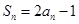 ,等差數列
,等差數列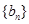 滿足
滿足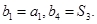
(1)求數列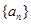
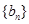 的通項公式
的通項公式
(2)設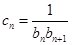 ,數列
,數列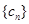 的前
的前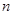 項和為
項和為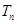 ,問
,問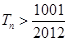 的最小正整數n是多少?
的最小正整數n是多少?
(1)an=2n-1,bn=2n-1(2)101
解析試題分析:(1)當n=1時,a1=S1=2a1-1,∴a1=1.
當n≥2時,an=Sn-Sn-1=(2an-1)-(2an-1-1)=2an-2an-1,即=2. ……2分
∴數列{an}是以a1=1為首項,2為公比的等比數列.
∴an=2n-1,Sn=2n-1. ……3分
設{bn}的公差為d,b1=a1=1,b4=1+3d=7,∴d=2.
∴bn=1+(n-1)×2=2n-1. ……6分
(2)∵cn===,
∴Tn=
==. ……10分
由Tn>,得>,解得n>100.1.
∴Tn>的最小正整數n是101. ……12分
考點:本小題主要考查等比的判斷和等差、等比數列的通項公式的求解,裂項法求數列是前n項和,考查學生的運算求解能力.
點評:判斷等差或等比數列時,一是用定義,一是用通項,不論用哪種方法,都不要忘記驗證n=1能否適合公式.


科目:高中數學 來源: 題型:解答題
已知曲線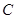 :
: ,數列
,數列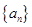 的首項
的首項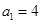 ,且
,且
當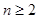 時,點
時,點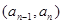 恒在曲線
恒在曲線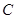 上,數列{
上,數列{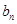 }滿足
}滿足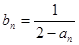
(1)試判斷數列 是否是等差數列?并說明理由;
是否是等差數列?并說明理由;
(2)求數列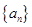 和
和 的通項公式;
的通項公式;
(3)設數列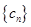 滿足
滿足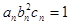 ,試比較數列
,試比較數列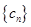 的前
的前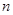 項和
項和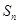 與
與 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分14分)
對數列{an},規定{△an}為數列{an}的一階差分數列,其中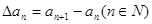 。
。
對自然數k,規定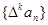 為{an}的k階差分數列,其中
為{an}的k階差分數列,其中 。
。
(1)已知數列{an}的通項公式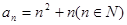 ,試判斷
,試判斷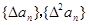 是否為等差或等比數列,為什么?
是否為等差或等比數列,為什么?
(2)若數列{an}首項a1=1,且滿足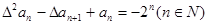 ,求數列{an}的通項公式。
,求數列{an}的通項公式。
(3)對(2)中數列{an},是否存在等差數列{bn},使得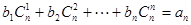 對一切自然
對一切自然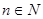 都成立?若存在,求數列{bn}的通項公式;若不存在,則請說明理由。
都成立?若存在,求數列{bn}的通項公式;若不存在,則請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)在數列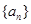 中,
中,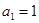 ,并且對于任意n∈N*,都有
,并且對于任意n∈N*,都有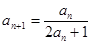 .
.
(1)證明數列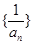 為等差數列,并求
為等差數列,并求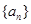 的通項公式;
的通項公式;
(2)設數列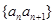 的前n項和為
的前n項和為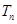 ,求使得
,求使得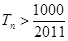 的最小正整數
的最小正整數 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
數列{an}滿足4a1=1,an-1=[(-1)nan-1-2]an(n≥2),(1)試判斷數列{1/an+(-1)n}是否為等比數列,并證明;(2)設an2?bn=1,求數列{bn}的前n項和Sn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com