
已知二次函數(shù)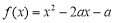 (
(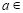 R).
R).
(1)解不等式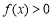 ;
;
(2)函數(shù)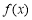 在
在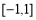 上有零點,求
上有零點,求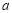 的取值范圍.
的取值范圍.
(1) 時,解集為R;
時,解集為R;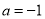 或
或 時,解集為
時,解集為 ;
;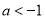 或
或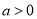 時,解集為
時,解集為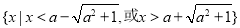 ;(2)
;(2)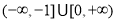 。
。
【解析】
試題分析:(1)這是一道含參數(shù)一元二次不等式問題,因為判別式含有參數(shù) ,需要對
,需要對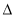 進行分類討論;
進行分類討論;
(2)思路一:函數(shù) 在
在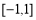 上有零點,即函數(shù)
上有零點,即函數(shù)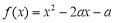 圖像在區(qū)間
圖像在區(qū)間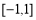 上與
上與 軸有交點,然后就交點的個數(shù)分類討論。思路二:函數(shù)
軸有交點,然后就交點的個數(shù)分類討論。思路二:函數(shù) 在
在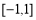 上有零點,即方程
上有零點,即方程
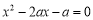 有根,可化為
有根,可化為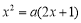 ,然后對
,然后對 進行討論,
進行討論, 不為零時,可化為
不為零時,可化為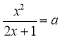 ,然后構造函數(shù)
,然后構造函數(shù) ,轉化為求該函數(shù)在
,轉化為求該函數(shù)在 上的最值問題。
上的最值問題。
試題解析:(1)方程 的判別式
的判別式 ,
,
當 時,
時, ,不等式
,不等式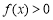 的解集為R;
的解集為R;
當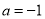 或
或 時,
時,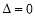 ,不等式
,不等式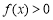 的解集為
的解集為 ;
;
當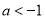 或
或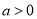 時,
時, ,
,
不等式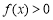 的解集為
的解集為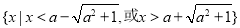 . 6分
. 6分
(2)法1:當 時,
時, 在
在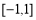 上有一個零點0;
上有一個零點0;
當 時,
時, 在
在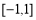 上有一個零點-1;
上有一個零點-1;
當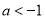 時,考慮到
時,考慮到 ,對稱軸
,對稱軸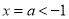 ,則有
,則有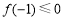 ,得
,得 ,
,
所以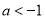 ;
;
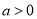 時,考慮到
時,考慮到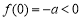 ,對稱軸
,對稱軸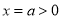 ,則有
,則有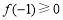 ,得
,得 ,
,
所以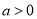 .
.
綜上,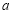 的取值范圍為
的取值范圍為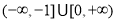 . 16分
. 16分
法2:由 ,得
,得 ①,
①,
對于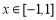 ,
,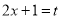 ,則
,則 ,
, ,變?yōu)?img src="http://thumb.zyjl.cn/pic6/res/GZSX/web/STSource/2015021506145168367441/SYS201502150615047622493821_DA/SYS201502150615047622493821_DA.042.png">②
,變?yōu)?img src="http://thumb.zyjl.cn/pic6/res/GZSX/web/STSource/2015021506145168367441/SYS201502150615047622493821_DA/SYS201502150615047622493821_DA.042.png">②
若 ,則②不成立,故可得
,則②不成立,故可得 ,
,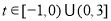 .
.
令 ,則
,則 .
.
當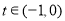 時,
時, ,
,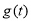 單調遞減;當
單調遞減;當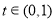 時,
時, ,
,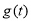 單調遞減;
單調遞減;
當 時,
時,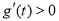 ,
,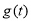 單調遞增.所以
單調遞增.所以 的值域為
的值域為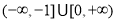 .
.
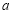 的取值范圍為
的取值范圍為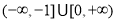 . 16分
. 16分
考點:(1)含參數(shù)一元二次不等式的解法;(2)一元二次方程根的分布問題;(3)構造函數(shù)及分類討論思想的應用。


科目:高中數(shù)學 來源:2015屆江西省南昌市三校高三10月聯(lián)考理科數(shù)學試卷(解析版) 題型:選擇題
已知 ,
, 是不共線的向量,若
是不共線的向量,若 =λ
=λ +
+ ,
, =
= +μ
+μ (λ,μ∈R),則A, B, C三點共線的充要條件是:( )
(λ,μ∈R),則A, B, C三點共線的充要條件是:( )
A.λ+μ=1 B.λ-μ=1 C.λμ=1 D.λμ=-1
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆江西省高三上學期第三次考試文科數(shù)學試卷(解析版) 題型:選擇題
不等式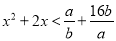 對任意
對任意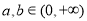 恒成立,則實數(shù)
恒成立,則實數(shù)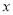 的取值范圍是
的取值范圍是
A.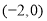 B.
B.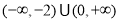
C.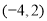 D.
D.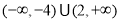
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆江蘇省連云港高二下學期期末數(shù)學試卷(選修物理)(解析版) 題型:填空題
將1、2、3、4、5、6、7、8、9這9個正整數(shù)分別寫在三張卡片上,要求每一張卡片上的三個數(shù)字中任意兩數(shù)之差都不在這張卡片上.現(xiàn)在第一張卡片上已經寫有1和5,第二張卡片上寫有2,第三張卡片上寫有3,則第一張卡片上的另外一個數(shù)字是 .
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆江蘇省連云港高二下學期期末數(shù)學試卷(選修物理)(解析版) 題型:填空題
二項式 的展開式中
的展開式中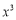 的系數(shù)為 .(用數(shù)字作答)
的系數(shù)為 .(用數(shù)字作答)
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆江蘇省連云港高二下學期期末數(shù)學試卷(選修歷史)(解析版) 題型:填空題
已知復數(shù)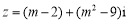 在復平面內對應的點位于第四象限,則實數(shù)
在復平面內對應的點位于第四象限,則實數(shù)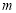 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆江蘇省蘇州市高三上學期期中測試數(shù)學試卷(解析版) 題型:解答題
(本題滿分14分)已知向量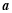
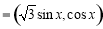 ,
,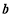
 ,
,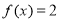
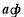
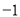 .
.
(1)求函數(shù)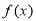 的單調遞減區(qū)間及其圖象的對稱軸方程;
的單調遞減區(qū)間及其圖象的對稱軸方程;
(2)當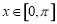 時,若
時,若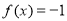 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆廣東省深圳市高三上學期第一次五校聯(lián)考文科數(shù)學試卷(解析版) 題型:解答題
已知函數(shù)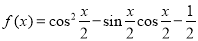
(1)求函數(shù) 的最小正周期和值域;
的最小正周期和值域;
(2)若 ,求
,求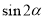 的值.
的值.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com