
已知Sn是正數數列{an}的前n項和,S12,S22、……、Sn2 ……,是以3為首項,以1為公差的等差數列;數列{bn}為無窮等比數列,其前四項之和為120,第二項與第四項之和為90。
(1)求an、bn;
(2)從數列{![]() }中能否挑出唯一的無窮等比數列,使它的各項和等于
}中能否挑出唯一的無窮等比數列,使它的各項和等于![]() 。若能的話,請寫出這個數列的第一項和公比?若不能的話,請說明理由。
。若能的話,請寫出這個數列的第一項和公比?若不能的話,請說明理由。
(1)an=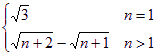 (n??N);bn=3n(n??N)(2)見解析
(n??N);bn=3n(n??N)(2)見解析
(1){Sn}是以3為首項,以1為公差的等差數列;所以Sn2=3+(n–1)=n+2
因為an>0,所以Sn=![]() (n??N),當n≥2時,an=Sn–Sn–1=
(n??N),當n≥2時,an=Sn–Sn–1=![]() –
–![]() ,又a1=S1=
,又a1=S1=![]() ,所以an=
,所以an=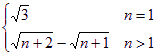 (n??N) ,設{bn}的首項為b1,公比為q,則有
(n??N) ,設{bn}的首項為b1,公比為q,則有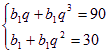 ,所以
,所以![]() ,所以bn=3n(n??N),
,所以bn=3n(n??N),
(2)![]() =(
=(![]() )n,設可以挑出一個無窮等比數列{cn},首項為c1=(
)n,設可以挑出一個無窮等比數列{cn},首項為c1=(![]() )p,公比為(
)p,公比為(![]() )k,(p、k??N), 它的各項和等于
)k,(p、k??N), 它的各項和等于![]() =
=![]() ,則有
,則有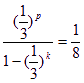 ,所以(
,所以(![]() )p=
)p=![]() [1–(
[1–(![]() )k], 當p≥k時3p–3p–k=8,即3p–k(3k–1)=8, 因為p、k??N,所以只有p–k=0,k=2時,即p=k=2時,數列{cn}的各項和為
)k], 當p≥k時3p–3p–k=8,即3p–k(3k–1)=8, 因為p、k??N,所以只有p–k=0,k=2時,即p=k=2時,數列{cn}的各項和為![]() 。當p<k時,3k–1=8.3k–p,因為k>p右邊含有3的因數,而左邊非3的倍數,不存在p、k??N,所以唯一存在等比數列{cn},首項為
。當p<k時,3k–1=8.3k–p,因為k>p右邊含有3的因數,而左邊非3的倍數,不存在p、k??N,所以唯一存在等比數列{cn},首項為![]() ,公比為
,公比為![]() ,使它的各項和等于
,使它的各項和等于![]() 。
。


科目:高中數學 來源: 題型:
| 1 |
| bn |
| 1 | ||
|
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)
(理)已知Sn是正數數列{an}的前n項和,S12,S22、……、Sn2 ……,是以3為首項,以1為公差的等差數列;數列{bn}為無窮等比數列,其前四項之和為120,第二項與第四項之和為90.
(I)求an、bn;(II)從數列{![]() }中能否挑出唯一的無窮等比數列,使它的各項和等于
}中能否挑出唯一的無窮等比數列,使它的各項和等于![]() .若能的話,請寫出這個數列的第一項和公比?若不能的話,請說明理由.
.若能的話,請寫出這個數列的第一項和公比?若不能的話,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
(Ⅰ)求an和bn;
(Ⅱ)試從數列{![]() }中挑出一些項構成一個無窮等比數列,使它的各項和等于
}中挑出一些項構成一個無窮等比數列,使它的各項和等于![]() ,并指出所挑數列的首項和公比.
,并指出所挑數列的首項和公比.
查看答案和解析>>
科目:高中數學 來源:2009-2010年上海市華東師大二附中高三數學綜合練習試卷(06)(解析版) 題型:解答題
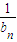 }中能否挑出唯一的無窮等比數列,使它的各項和等于
}中能否挑出唯一的無窮等比數列,使它的各項和等于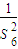 .若能的話,請寫出這個數列的第一項和公比?若不能的話,請說明理由.
.若能的話,請寫出這個數列的第一項和公比?若不能的話,請說明理由.查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com