【答案】
分析:(1)記F(x)=sinx-
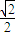
x,可求得F′(x)=cosx-

,分x∈(0,

)與x∈(

,1)兩類討論,可證得當x∈[0,1]時,F(x)≥0,即sinx≥
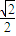
x;記H(x)=sinx-x,同理可證當x∈(0,1)時,sinx≤x,二者結合即可證得結論;
(2)利用(1),可求得當x∈[0,1]時,ax+x
2+
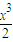
+2(x+2)cosx-4≤(a+2)x,分a≤-2與a>-2討論即可求得實數a的取值范圍.
解答:(1)證明:記F(x)=sinx-

x,則F′(x)=cosx-
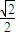
.
當x∈(0,
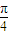
)時,F′(x)>0,F(x)在[0,
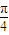
]上是增函數;
當x∈(
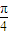
,1)時,F′(x)<0,F(x)在[
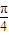
,1]上是減函數;
又F(0)=0,F(1)>0,所以當x∈[0,1]時,F(x)≥0,即sinx≥
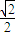
x…3
記H(x)=sinx-x,則當x∈(0,1)時,H′(x)=cosx-1<0,所以H(x)在[0,1]上是減函數;則H(x)≤H(0)=0,
即sinx≤x.
綜上,
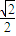
x≤sinx≤x…5
(2)∵當x∈[0,1]時,ax+x
2+
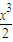
+2(x+2)cosx-4
=(a+2)x+x
2+
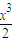
-4(x+2)
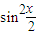
≤(a+2)x+x
2+
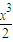
-4(x+2)
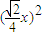
=(a+2)x,
∴當a≤-2時,不等式ax+x
2+
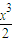
+2(x+2)cosx≤4對x∈[0,1]恒成立,…9
下面證明,當a>-2時,不等式ax+x
2+
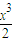
+2(x+2)cosx≤4對x∈[0,1]不恒成立.
∵當x∈[0,1]時,ax+x
2+
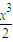
+2(x+2)cosx-4
=(a+2)x+x
2+
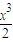
-4(x+2)
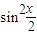
≥(a+2)x+x
2+
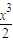
-4(x+2)
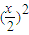
=(a+2)x-x
2-
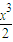
≥(a+2)x-

x
2=-

x[x-

(a+2)].
所以存在x
∈(0,1)(例如x
取

和

中的較小值)滿足
ax
+
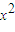
+

+2(x
+2)cosx
-4>0,
即當a>-2時,不等式ax+x
2+
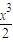
+2(x+2)cosx≤4對x∈[0,1]不恒成立.
綜上,實數a的取值范圍是(-∞,-2].
點評:本題考查不等式的證明,突出考查利用導數研究函數的單調性及函數恒成立問題,考查分類討論思想與等價轉化思想的綜合應用,屬于難題.

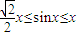 ;
; 對x∈[0,1]恒成立,求實數a的取值范圍.
對x∈[0,1]恒成立,求實數a的取值范圍.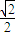 x,可求得F′(x)=cosx-
x,可求得F′(x)=cosx- ,分x∈(0,
,分x∈(0, )與x∈(
)與x∈( ,1)兩類討論,可證得當x∈[0,1]時,F(x)≥0,即sinx≥
,1)兩類討論,可證得當x∈[0,1]時,F(x)≥0,即sinx≥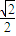 x;記H(x)=sinx-x,同理可證當x∈(0,1)時,sinx≤x,二者結合即可證得結論;
x;記H(x)=sinx-x,同理可證當x∈(0,1)時,sinx≤x,二者結合即可證得結論;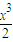 +2(x+2)cosx-4≤(a+2)x,分a≤-2與a>-2討論即可求得實數a的取值范圍.
+2(x+2)cosx-4≤(a+2)x,分a≤-2與a>-2討論即可求得實數a的取值范圍. x,則F′(x)=cosx-
x,則F′(x)=cosx-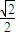 .
.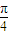 )時,F′(x)>0,F(x)在[0,
)時,F′(x)>0,F(x)在[0,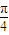 ]上是增函數;
]上是增函數;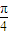 ,1)時,F′(x)<0,F(x)在[
,1)時,F′(x)<0,F(x)在[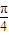 ,1]上是減函數;
,1]上是減函數;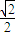 x…3
x…3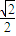 x≤sinx≤x…5
x≤sinx≤x…5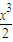 +2(x+2)cosx-4
+2(x+2)cosx-4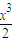 -4(x+2)
-4(x+2)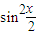
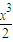 -4(x+2)
-4(x+2)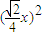
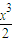 +2(x+2)cosx≤4對x∈[0,1]恒成立,…9
+2(x+2)cosx≤4對x∈[0,1]恒成立,…9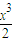 +2(x+2)cosx≤4對x∈[0,1]不恒成立.
+2(x+2)cosx≤4對x∈[0,1]不恒成立.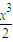 +2(x+2)cosx-4
+2(x+2)cosx-4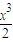 -4(x+2)
-4(x+2)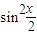
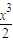 -4(x+2)
-4(x+2)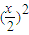
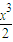
 x2
x2 x[x-
x[x- (a+2)].
(a+2)]. 和
和 中的較小值)滿足
中的較小值)滿足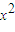 +
+ +2(x+2)cosx-4>0,
+2(x+2)cosx-4>0,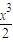 +2(x+2)cosx≤4對x∈[0,1]不恒成立.
+2(x+2)cosx≤4對x∈[0,1]不恒成立.

