
若圓![]() 過點
過點![]() 且與直線
且與直線![]() 相切,設圓心
相切,設圓心![]() 的軌跡為曲線
的軌跡為曲線![]() ,
,![]() 、
、![]() 為曲線
為曲線![]() 上的兩點,點
上的兩點,點![]() ,且滿足
,且滿足![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,過
,過![]() 、
、![]() 兩點的圓
兩點的圓![]() 與拋物線在點
與拋物線在點![]() 處有共同的切線,求圓
處有共同的切線,求圓![]() 的方程;
的方程;
(3)分別過![]() 、
、![]() 作曲線
作曲線![]() 的切線,兩條切線交于點
的切線,兩條切線交于點![]() ,若點
,若點![]() 恰好在直線
恰好在直線![]() 上,求證:
上,求證:![]() 與
與![]() 均為定值.
均為定值.
21.解:(1)依題意,點![]() 到定點
到定點![]() 的距離等于到定直線
的距離等于到定直線![]() 的距離,所以點
的距離,所以點![]() 的軌跡為拋物線,曲線
的軌跡為拋物線,曲線![]() 的方程為
的方程為![]() ; …………………………………………………………3分
; …………………………………………………………3分
(2)直線![]() 的方程是
的方程是![]() ,即
,即![]() ,
,
由![]() 得點
得點![]() 、
、![]() 的坐標是
的坐標是![]() 或
或![]() ,………………………………5分
,………………………………5分
當![]() 、
、![]() 時,由
時,由![]() 得
得![]() ,
,![]() ,
,
所以拋物線![]() 在點
在點![]() 處切線的斜率為
處切線的斜率為![]() ,
,
直線![]() 的方程為
的方程為![]() ,即
,即![]() …………①
…………①
線段![]() 的中點坐標為
的中點坐標為![]() ,中垂線方程為
,中垂線方程為![]() ,即
,即![]() …………②
…………②
由①、②解得![]() , …………………………………………………………7分
, …………………………………………………………7分
于是,圓![]() 的方程為
的方程為![]() ,
,
即 ![]() , ………………………………………………………8分
, ………………………………………………………8分
當![]() 、
、![]() 時,拋物線
時,拋物線![]() 在點
在點![]() 處切線的斜率為
處切線的斜率為![]() ,此時切線與
,此時切線與![]() 垂直,所求圓為以
垂直,所求圓為以![]() 為直徑的圓,可求得圓為
為直徑的圓,可求得圓為![]() , ……9分
, ……9分
(3)設![]() ,
,![]() ,
,![]() ,過點
,過點![]() 的切線方程為
的切線方程為![]() ,
,
即![]() ,同理可得
,同理可得![]() ,所以
,所以![]() ,
,![]() ,……10分
,……10分
又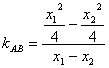 =
=![]() ,所以直線
,所以直線![]() 的方程為
的方程為![]() ,
,
即![]() ,亦即
,亦即![]() ,所以
,所以![]() ,………………………………………11分
,………………………………………11分
而![]() ,
,![]() ,所以
,所以
![]()
![]()
![]() . …………………………………13分
. …………………………………13分


科目:高中數學 來源:2011-2012學年甘肅省高三百題集理科數學試卷(解析版)(四) 題型:解答題
若圓 過點
過點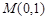 且與直線
且與直線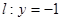 相切,設圓心
相切,設圓心 的軌跡為曲線
的軌跡為曲線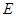 ,
, 、
、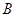 為曲線
為曲線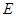 上的兩點,點
上的兩點,點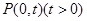 ,且滿足
,且滿足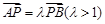 .
.
(1)求曲線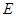 的方程;
的方程;
(2)若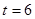 ,直線
,直線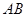 的斜率為
的斜率為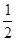 ,過
,過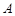 、
、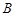 兩點的圓
兩點的圓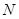 與拋物線在點
與拋物線在點 處有共同的切線,求圓
處有共同的切線,求圓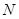 的方程;
的方程;
(3)分別過 、
、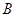 作曲線
作曲線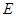 的切線,兩條切線交于點
的切線,兩條切線交于點 ,若點
,若點 恰好在直線
恰好在直線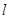 上,求證:
上,求證: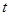 與
與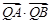 均為定值.
均為定值.
查看答案和解析>>
科目:高中數學 來源:2010年普通高等學校招生全國統一考試(重慶卷)數學文史類模擬試卷(三) 題型:解答題
已知動圓P過點 且與直線
且與直線 相切.
相切.
(Ⅰ) 求動圓圓心P的軌跡E的方程;
(Ⅱ) 設直線 與軌跡E交于點A、B,M是線段AB的中點,過M作
與軌跡E交于點A、B,M是線段AB的中點,過M作 軸的垂線交軌跡E于N.
軸的垂線交軌跡E于N.
① 證明:軌跡E點N處的切線 與AB平行;
與AB平行;
② 是否存在實數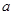 ,使
,使 ?若存在,求
?若存在,求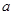 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
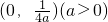 且與直線
且與直線 相切.
相切.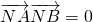 ?若存在,求a的值;若不存在,說明理由.
?若存在,求a的值;若不存在,說明理由.查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分13分)若圓![]() 過點
過點![]() 且與直線
且與直線![]() 相切,設圓心
相切,設圓心![]() 的軌跡為曲線
的軌跡為曲線![]() ,
,![]() 、
、![]() 為曲線
為曲線![]() 上的兩點,點
上的兩點,點![]() ,且滿足
,且滿足![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,過
,過![]() 、
、![]() 兩點的圓
兩點的圓![]() 與拋物線在點
與拋物線在點![]() 處有共同的切線,求圓
處有共同的切線,求圓![]() 的方程;
的方程;
(3)分別過![]() 、
、![]() 作曲線
作曲線![]() 的切線,兩條切線交于點
的切線,兩條切線交于點![]() ,若點
,若點![]() 恰好在直線
恰好在直線![]() 上,求證:
上,求證:![]() 與
與![]() 均為定值.
均為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com