
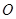 的直線
的直線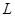 與拋物線
與拋物線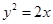 相交于
相交于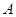 、
、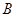 兩點,且
兩點,且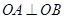 ,
,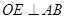 于
于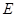 .
.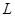 過定點;
過定點; 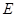 的軌跡方程.
的軌跡方程.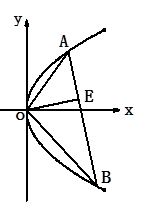
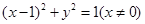 .
.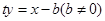 ,然后根據題目給的方程條件
,然后根據題目給的方程條件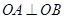 ,即可確定b的值或找到b與t的關系,進而確定定點.
,即可確定b的值或找到b與t的關系,進而確定定點.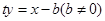 與拋物線
與拋物線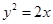 相交于
相交于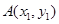 、
、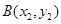 兩點
兩點 ……………………2分
……………………2分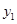 、
、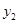 是此方程的兩實根,由韋達定理得:
是此方程的兩實根,由韋達定理得: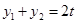
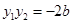 ……………………3分
……………………3分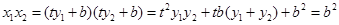 …………4分
…………4分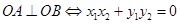 ……………………5分
……………………5分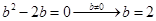 ……………………6分
……………………6分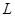 :
: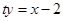 過定點
過定點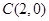 ……………………8分
……………………8分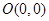 ,
,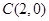 ,
,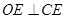 ……………………9分
……………………9分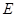 的軌跡是以線段
的軌跡是以線段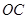 為直徑的圓除去點
為直徑的圓除去點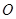 , ……………………11分
, ……………………11分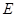 的軌跡方程為
的軌跡方程為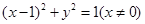 ……………………12分
……………………12分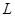 的方程設為
的方程設為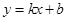 又沒有討論
又沒有討論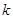 不存在的情況扣2分;軌跡方程中沒有限制
不存在的情況扣2分;軌跡方程中沒有限制 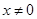 扣1分.
扣1分.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com