
【題目】水污染現狀與工業廢水排放密切相關,某工廠深人貫徹科學發展觀,努力提高污水收集處理水平,其污水處理程序如下:原始污水必先經過A系統處理,處理后的污水(A級水)達到環保標準(簡稱達標)的概率為p(0<p<1).經化驗檢測,若確認達標便可直接排放;若不達標則必須進行B系統處理后直接排放.
某廠現有4個標準水量的A級水池,分別取樣、檢測,多個污水樣本檢測時,既可以逐個化驗,也可以將若干個樣本混合在一起化驗,混合樣本中只要有樣本不達標,則混合樣本的化驗結果必不達標,若混合樣本不達標,則該組中各個樣本必須再逐個化驗;若混合樣本達標,則原水池的污水直接排放
現有以下四種方案:
方案一:逐個化驗;
方案二:平均分成兩組化驗;方案三;三個樣本混在一起化驗,剩下的一個單獨化驗;
方案四:四個樣本混在一起化驗.
化驗次數的期望值越小,則方案越"優".
(1)若![]() ,求2個A級水樣本混合化驗結果不達標的概率;
,求2個A級水樣本混合化驗結果不達標的概率;
(2)①若![]() ,現有4個A級水樣本需要化驗,請問:方案一、二、四中哪個最“優"?②若“方案三”比“方案四"更“優”,求p的取值范圍.
,現有4個A級水樣本需要化驗,請問:方案一、二、四中哪個最“優"?②若“方案三”比“方案四"更“優”,求p的取值范圍.
【答案】(1)![]() ;(2)①方案四最優;②
;(2)①方案四最優;②![]()
【解析】
(1)計算2個A級混合樣本達標的概率,再根據對立事件原理求得它們不達標的概率;
(2)①計算方案一:逐個檢測,檢測次數為ξ=4;方案二:檢測次數為ξ2,則ξ2可能取值為2,4,6,求概率分布列,計算數學期望;方案四:混在一起檢測,檢測次數為ξ4,則ξ4可取值為1,5,求概率分布列,計算數學期望;比較得出選擇方案幾最“優”;
②方案三:化驗次數為η3,則η3可取值為2,5,求概率分布列,計算數學期望;
方案四:化驗次數為η4,則η4可取值為1,5,求概率分布,計算數學期望;
由題意列不等式E(η3)<E(η4),求出p的取值范圍.
(1)該混合樣本達標的概率是![]() ,所以根據對立事件原理,不達標的概率為
,所以根據對立事件原理,不達標的概率為![]() .
.
(2)①方案一:逐個檢測,檢測次數為4.
方案二:由(1)知,每組兩個樣本檢測時,若達標則檢測次數為1,概率為![]() ;若不達標則檢測次數為3,概率為
;若不達標則檢測次數為3,概率為![]() .故方案二的檢測次數記為ξ2,ξ2的可能取值為2,4,6.
.故方案二的檢測次數記為ξ2,ξ2的可能取值為2,4,6.
其分布列如下,
|
|
|
|
|
|
|
|
可求得方案二的期望為![]()
方案四:混在一起檢測,記檢測次數為ξ4,ξ4可取1,5.
其分布列如下,
|
|
|
|
|
|
可求得方案四的期望為![]() .
.
比較可得![]() ,故選擇方案四最“優”.
,故選擇方案四最“優”.
②方案三:設化驗次數為![]() ,
,![]() 可取2,5.
可取2,5.
|
|
|
|
|
|
![]() ;
;
方案四:設化驗次數為![]() ,
,![]() 可取
可取![]()
|
|
|
|
|
|
![]() ;
;
由題意得![]() .
.
故當![]() 時,方案三比方案四更“優”.
時,方案三比方案四更“優”.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,菱形ABCD的邊長為a,∠D=60°,點H為DC邊中點,現以線段AH為折痕將△DAH折起使得點D到達點P的位置且平面PHA⊥平面ABCH,點E,F分別為AB,AP的中點.

(1)求證:平面PBC∥平面EFH;
(2)若三棱錐P﹣EFH的體積等于![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在直角梯形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 在
在![]() 上,且
上,且![]() ,將
,將![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如圖2).
(如圖2).![]() 為
為![]() 中點
中點
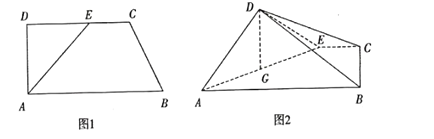
(1)求證:![]() ;
;
(2)求四棱錐![]() 的體積;
的體積;
(3)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,請說明理由
的值;若不存在,請說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】互聯網使我們的生活日益便捷,網絡外賣也開始成為不少人日常生活中不可或缺的一部分,某市一調查機構針對該市市場占有率較高的甲、乙兩家網絡外賣企業(以下外賣甲、外賣乙)的經營情況進行了調查,調查結果如下表:
1日 | 2日 | 3日 | 4日 | 5日 | |
外賣甲日接單x(百單) | 5 | 2 | 9 | 8 | 11 |
外賣乙日接單y(百單) | 2 | 3 | 10 | 5 | 15 |
(1)試根據表格中這五天的日接單量情況,從統計的角度說明這兩家外賣企業的經營狀況;
(2)據統計表明,y與x之間具有線性關系.
①請用相關系數r對y與x之間的相關性強弱進行判斷;(若![]() ,則可認為y與x有較強的線性相關關系(r值精確到0.001))
,則可認為y與x有較強的線性相關關系(r值精確到0.001))
②經計算求得y與x之間的回歸方程為![]() ,假定每單外賣業務企業平均能獲純利潤3元,試預測當外賣乙日接單量不低于25百單時,外賣甲所獲取的日純利潤的大致范圍.(x值精確到0.01)
,假定每單外賣業務企業平均能獲純利潤3元,試預測當外賣乙日接單量不低于25百單時,外賣甲所獲取的日純利潤的大致范圍.(x值精確到0.01)
相關公式: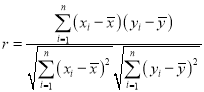 ,
,
參考數據: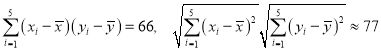 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,
(Ⅰ)若在函數![]() 的定義域內存在區間
的定義域內存在區間![]() ,使得該函數在區間
,使得該函數在區間![]() 上為減函數,求實數
上為減函數,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)當![]() 時,若曲線
時,若曲線![]() 在點
在點![]() 處的切線
處的切線![]() 與曲線
與曲線![]() 有且只有一個公共點,求實數
有且只有一個公共點,求實數![]() 的值或取值范圍.
的值或取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求函數![]() 的圖象在點
的圖象在點![]() 處的切線方程;
處的切線方程;
(2)若![]() 在
在![]() 上有解,求
上有解,求![]() 的取值范圍;
的取值范圍;
(3)設![]() 是函數
是函數![]() 的導函數,
的導函數,![]() 是函數
是函數![]() 的導函數,若函數
的導函數,若函數![]() 的零點為
的零點為![]() ,則點
,則點![]() 恰好就是該函數
恰好就是該函數![]() 的對稱中心.試求
的對稱中心.試求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知BD為圓錐AO底面的直徑,若![]() ,C是圓錐底面所在平面內一點,
,C是圓錐底面所在平面內一點,![]() ,且AC與圓錐底面所成角的正弦值為
,且AC與圓錐底面所成角的正弦值為![]() .
.
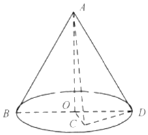
(1)求證:平面![]() 平面ACD;
平面ACD;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com