【題目】某地區隨著經濟的發展，居民收入逐年增長，銀行儲蓄連年增長，下表是該地區某銀行連續五年的儲蓄存款（年底結算）：
年份 |
|
|
|
|
|
儲蓄存款 |
|
|
|
|
|
為方便研究，工作人員對上表的數據做了如下處理：
，
得到下表：
|
|
|
|
|
|
|
|
|
|
|
|
（1）用最小二乘法求出
關于
的線性回歸方程
；
（2）通過（1）中的方程，求出
關于
的線性回歸方程，并用所求回歸方程預測
年底，該地儲蓄存款額可達多少？
（附：參考公式，其中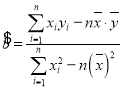
，
）
科目：高中數學 來源： 題型：
【題目】下列命題中錯誤的是
A. 若命題p為真命題,命題q為假命題,則命題“pV(q)”為真命題
B. 命題“若a+b≠7,則a≠2或b≠5”為真命題
C. 命題“若x2-x=0,則x=0或x=1”的否命題為“若x2-x=0,則x≠0且x≠1”
D. 命題p: 
x>0,sinx>2x-1,則
p為
x>0,sinx≤2x-1
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在2016年8月巴西里約熱內盧舉辦的第31屆奧運會上，乒乓球比賽團體決賽實行五場三勝制，且任何一方獲勝三場比賽即結束.甲、乙兩個代表隊最終進入決賽，根據雙方排定的出場順序及以往戰績統計分析，甲隊依次派出的五位選手分別戰勝對手的概率如下表：
出場順序 | 1號 | 2號 | 3號 | 4號 | 5號 |
獲勝概率 |
|
|
|
|
|
若甲隊橫掃對手獲勝（即3∶0獲勝）的概率是
，比賽至少打滿4場的概率為
.
（1）求
，
的值；
（2）求甲隊獲勝場數的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）＝axex﹣lnx﹣x．
（Ⅰ）若f（x）有兩個不同的零點，求實數a的取值范圍；
（Ⅱ）已知a＝1，若對任意的x＞0，均有f（x）＞cx2﹣2x+1成立，求實數c的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下圖是我國2008年至2014年生活垃圾無害化處理量（單位：億噸）的折線圖.
（Ⅰ）由折線圖看出，可用線性回歸模型擬合y與t的關系，請用相關系數加以說明；
（Ⅱ）建立y關于t的回歸方程（系數精確到0.01），預測2016年我國生活垃圾無害化處理量.
附注：
參考數據：
，
，
，
≈2.646.
參考公式：相關系數
回歸方程
中斜率和截距的最小二乘估計公式分別為：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設定義在R上的函數
，當
時，
取極大值
，且函數
的圖象關于原點對稱．
（1）求的表達式；
（2）試在函數的圖象上求兩點，使以這兩點為切點的切線互相垂直，且切點的橫坐標都在
上；
（3）設
，
，求證：
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
