與圓(x+3)2+y2=1及圓(x-3)2+y2=9都外切的圓的圓心軌跡方程為 .
【答案】
分析:設所求圓的圓心坐標P(x,y),半徑為r,兩圓的圓心分別是C
1,C
2,根據(jù)題意可知兩圓心的坐標,根據(jù)所求圓與兩個圓都外切進而可得PC
1|和|PC
2|的表達式,整理可得|PC
2|-|PC
1|=2,根據(jù)雙曲線定義可知P點的軌跡為C
1,C
2為焦點的雙曲線進而根據(jù)雙曲線的性質(zhì)可求得雙曲線的方程.
解答:解:設所求圓的圓心坐標P(x,y),半徑為r,兩圓的圓心分別是C
1,C
2,
∵所求圓與兩個圓都外切,
∴|PC
1|=r+1,|PC
2|=r+3,
即|PC
2|-|PC
1|=2,
根據(jù)雙曲線定義可知P點的軌跡為以C
1,C
2為焦點的雙曲線,2c=6,c=3;2a=2,a=1,b=2
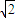
∴P點的軌跡方程為
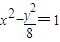
(x<0)
故答案為:為
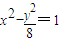
(x<0)
點評:本題主要考查點的軌跡方程及雙曲線的性質(zhì).常用方法是直接法,定義法,代入轉(zhuǎn)移法等.

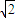
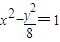 (x<0)
(x<0)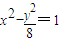 (x<0)
(x<0)
