
【題目】已知![]() ,
,
(1)若展開式中第5項,第6項與第7項的二項式系數成等差數列,求展開式中二項式系數最大項
的系數;
(2)若展開式前三項的二項式系數和等于79,求展開式中系數最大的項.
【答案】(1)70(2)![]() (2x)10
(2x)10
【解析】
試題分析:(1)第k+1項的二項式系數為![]() ,由題意可得關于n的方程,求出n.而二項式系數最大的項為中間項,n為奇數時,中間兩項二項式系數相等;n為偶數時,中間只有一項.(2)由展開式前三項的二項式系數和等于79,可得關于n的方程,求出n.而求展開式中系數最大的項時,可通過解不等式組求得,假設
,由題意可得關于n的方程,求出n.而二項式系數最大的項為中間項,n為奇數時,中間兩項二項式系數相等;n為偶數時,中間只有一項.(2)由展開式前三項的二項式系數和等于79,可得關于n的方程,求出n.而求展開式中系數最大的項時,可通過解不等式組求得,假設![]() 項的系數最大,
項的系數最大,![]() 項的系數為
項的系數為![]() ,則有
,則有
試題解析:(1)通項Tr+1=![]()
![]() n-r·(2x)r=22r-n
n-r·(2x)r=22r-n![]() xr,(此題可以用組合數表示結果)
xr,(此題可以用組合數表示結果)
由題意知![]() ,
,![]() ,
,![]() 成等差數列,
成等差數列,
∴![]() =
=![]() ,∴n=14或7.
,∴n=14或7.
當n=14時,第8項的二項式系數最大,該項的系數為22×7-14![]() =3 432;
=3 432;
當n=7時,第4、5項的二項式系數相等且最大,
其系數分別為22×3-7![]() =
=![]() ,22×4-7
,22×4-7![]() =70.
=70.
(2)由題意知![]() =79,
=79,
∴n=12或n=-13(舍).
∴Tr+1=22r-12![]() xr.
xr.
由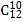 得
得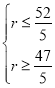 ∴r=10.
∴r=10.
∴展開式中系數最大的項為T11=22×10-12·![]() x10=
x10=![]() (2x)10. /p>
(2x)10. /p>


科目:高中數學 來源: 題型:
【題目】已知公差大于0的等差數列![]() 的前n項和為
的前n項和為![]() ,且滿足
,且滿足![]() ,
,![]() .
.
(1)求數列![]() 的通項公式
的通項公式![]() ;
;
(2)若![]() ,求
,求![]() 的表達式;
的表達式;
(3)若![]() ,存在非零常數
,存在非零常數![]() ,使得數列
,使得數列![]() 是等差數列,存在
是等差數列,存在![]() ,不等式
,不等式![]() 成立,求k的取值范圍.
成立,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近幾年出現各種食品問題,食品添加劑會引起血脂增高、血壓增高、血糖增高等疾病.為了解三高疾病是否與性別有關,醫院隨機對入院的60人進行了問卷調查,得到了如圖的列聯表:
患三高疾病 | 不患三高疾病 | 合計 | |
男 | 6 | 30 | |
女 | |||
合計 | 36 |
(1)請將如圖的列聯表補充完整;若用分層抽樣的方法在患三高疾病的人群中抽![]() 人,其中女性抽多少人?
人,其中女性抽多少人?
(2)為了研究三高疾病是否與性別有關,請計算出統計量![]() ,并說明你有多大的把握認為三高疾病與性別有關?
,并說明你有多大的把握認為三高疾病與性別有關?
下面的臨界值表供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式![]()
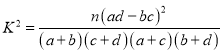 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】自古以來“民以食為天”,餐飲業作為我國第三產業中的一個支柱產業,一直在社會發展與人民生活中發揮著重要作用.某機構統計了2010~2016年餐飲收入的情況,得到下面的條形圖,則下面結論中不正確的是( )

A. 2010~2016年全國餐飲收入逐年增加
B. 2016年全國餐飲收入比2010年翻了一番以上
C. 2010~2016年全國餐飲收入同比增量最多的是2015年
D. 2010~2016年全國餐飲收入同比增量超過3000億元的年份有3個
查看答案和解析>>
科目:高中數學 來源: 題型:
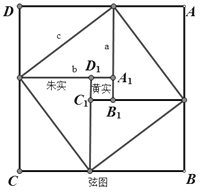
【題目】“勾股定理”在西方被稱為“畢達哥拉斯定理”,三國時期吳國的數學家趙爽在《周髀算經》中注釋了其理論證明,其基本思想是圖形經過割補后面積不變.即通過如圖所示的“弦圖”,將勻股定理表述為:“勾股各自乘,并之,為弦實,開方除之,即弦”(其中![]() 分別為勾股弦);證明方法敘述為:“按弦圖,又可以勾股相乘為朱實二,倍之為朱實四,以勾股之差自相乘為中黃實,加差實,亦成弦實”,即
分別為勾股弦);證明方法敘述為:“按弦圖,又可以勾股相乘為朱實二,倍之為朱實四,以勾股之差自相乘為中黃實,加差實,亦成弦實”,即![]() ,化簡得
,化簡得![]() .現已知
.現已知![]() ,
,![]() ,向外圍大正方形
,向外圍大正方形![]() 區域內隨機地投擲一枚飛鏢,飛鏢落在中間小正方形
區域內隨機地投擲一枚飛鏢,飛鏢落在中間小正方形![]() 內的概率是( )
內的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)試問:在![]() 軸的正半軸上是否存在一點
軸的正半軸上是否存在一點![]() ,使得
,使得![]() 的外心在
的外心在![]() 上?若存在,求
上?若存在,求![]() 的坐標;若不存在,請說明理由..
的坐標;若不存在,請說明理由..
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班50名學生期中考試數學成績的頻率分布直方圖如圖所示,其中成績分組區間是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].從樣本成績不低于80分的學生中隨機選取2人,記這2人成績在90分以上(含90分)的人數為ξ,則ξ的數學期望為( )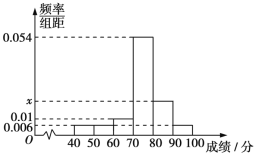
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com