
【題目】已知橢圓![]() 的離心率為
的離心率為![]() 為其左、右頂點,
為其左、右頂點,![]() 為橢圓上除
為橢圓上除![]() 外任意一點,若記直線
外任意一點,若記直線![]() 的斜率分別為
的斜率分別為![]()
(1)求證:![]() 為定值;
為定值;
(2)若橢圓![]() 的長軸長為
的長軸長為![]() ,過點
,過點![]() 作兩條互相垂直的直線
作兩條互相垂直的直線![]() ,,若
,,若![]() 恰好為
恰好為![]() 與橢圓相交的弦的中點,設
與橢圓相交的弦的中點,設![]() 為
為![]() 與橢圓相交的弦的中點,求線段
與橢圓相交的弦的中點,求線段![]() 的長.
的長.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求函數![]() 的最小正周期;
的最小正周期;
(2)將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度,再向下平移
個單位長度,再向下平移![]() (
(![]() )個單位長度后得到函數
)個單位長度后得到函數![]() 的圖象,且函數
的圖象,且函數![]() 的最大值為2.
的最大值為2.
(ⅰ)求函數![]() 的解析式; (ⅱ)證明:存在無窮多個互不相同的正整數
的解析式; (ⅱ)證明:存在無窮多個互不相同的正整數![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正項數列![]() 滿足:
滿足:![]() ,
,![]() ,其中
,其中![]() .
.
(1)若![]() ,求數列
,求數列![]() 的前
的前![]() 項的和;
項的和;
(2)若![]() ,
,![]() .
.
①求數列![]() 的通項公式;
的通項公式;
②記數列![]() 的前
的前![]() 項的和為
項的和為![]() ,若無窮項等比數列
,若無窮項等比數列![]() 始終滿足
始終滿足![]() ,求數列
,求數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某調查機構對全國互聯網行業進行調查統計,得到整個互聯網行業從業者年齡分布餅狀圖,90后從事互聯網行業崗位分布條形圖,則下列結論中不正確的是( )
注:90后指1990年及以后出生,80后指1980-1989年之間出生,80前指1979年及以前出生.


A.互聯網行業從業人員中90后占一半以上
B.互聯網行業中從事技術崗位的人數超過總人數的![]()
C.互聯網行業中從事運營崗位的人數90后比80前多
D.互聯網行業中從事技術崗位的人數90后比80后多
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,左、右頂點分別為A,B,點M是橢圓C上異于A,B的一點,直線AM與y軸交于點P.
,左、右頂點分別為A,B,點M是橢圓C上異于A,B的一點,直線AM與y軸交于點P.
(Ⅰ)若點P在橢圓C的內部,求直線AM的斜率的取值范圍;
(Ⅱ)設橢圓C的右焦點為F,點Q在y軸上,且∠PFQ=90°,求證:AQ∥BM.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,過點
中,過點![]() 作傾斜角為
作傾斜角為![]() 的直線
的直線![]() ,以原點
,以原點![]() 為極點,
為極點,![]() 軸非負半軸為極軸建立極坐標系,曲線
軸非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,將曲線
,將曲線![]() 上各點的橫坐標伸長為原來的2倍,縱坐標不變,得到曲線
上各點的橫坐標伸長為原來的2倍,縱坐標不變,得到曲線![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于不同的兩點
交于不同的兩點![]() .
.
(1)求直線![]() 的參數方程和曲線
的參數方程和曲線![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】同程旅游隨機調查了年齡在![]() (單位:歲)內的1250人的購票情況,其中50歲以下(不包含50歲)的有900人,50歲以上(包含50歲)的有350人,由調查數據的統計結果顯示,有
(單位:歲)內的1250人的購票情況,其中50歲以下(不包含50歲)的有900人,50歲以上(包含50歲)的有350人,由調查數據的統計結果顯示,有![]() 的人參與網上購票,網上購票人數的頻率分布直方圖如下圖所示.
的人參與網上購票,網上購票人數的頻率分布直方圖如下圖所示.

(1)已知年齡在![]() ,
,![]() ,
,![]() 的網上購票人數成等差數列,求
的網上購票人數成等差數列,求![]() 的值;
的值;
(2)根據題目數據填寫![]() 列聯表,并根據填寫數據判斷能否在犯錯誤的概率不超過0.001的前提下,認為網上購票與年齡有關系?
列聯表,并根據填寫數據判斷能否在犯錯誤的概率不超過0.001的前提下,認為網上購票與年齡有關系?
50歲以下 | 50歲以上 | 總計 | |
參與網上購票 | |||
不參與網上購票 | |||
總計 |
附: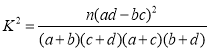
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
(3)為鼓勵大家網上購票,該平臺常采用購票就發放酒店入住代金券的方法進行促銷,具體做法如下:年齡在![]() 歲的每人發放20元,其余年齡段的每人發放50元,先按發放代金券的金額采用分層抽樣的方式從參與調查的1000位網上購票者中抽取10人,并在這10人中隨機抽取3人進行回訪調查,求此3人獲得代金券的金額總和
歲的每人發放20元,其余年齡段的每人發放50元,先按發放代金券的金額采用分層抽樣的方式從參與調查的1000位網上購票者中抽取10人,并在這10人中隨機抽取3人進行回訪調查,求此3人獲得代金券的金額總和![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在平面直角坐標系xOy中,直線l的參數方程為![]() (t為參數),曲線
(t為參數),曲線![]() 的方程為
的方程為![]() .以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系.
.以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系.
(1)求直線l和曲線![]() 的極坐標方程;
的極坐標方程;
(2)曲線![]() 分別交直線l和曲線
分別交直線l和曲線![]() 于點A,B,求
于點A,B,求![]() 的最大值及相應
的最大值及相應![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)![]() 為曲線
為曲線![]() 上的動點,點
上的動點,點![]() 在線段
在線段![]() 上,且滿足
上,且滿足![]() ,求點
,求點![]() 的軌跡
的軌跡![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 的極坐標為
的極坐標為![]() ,點
,點![]() 在曲線
在曲線![]() 上,求
上,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com