日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

如圖，△ABC與△BCD是一副三角板，它們所在的兩個平面互相垂直．若AB＝AC，∠BAC＝∠BCD＝90°，∠CBD＝30°．

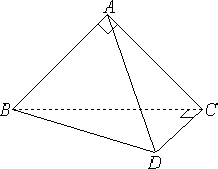
(Ⅰ)求證：三棱錐A－BCD的四個面都是直角三角形；

(Ⅱ)求二面角A－BD－C的正切值．

答案：利用點線面位置關系
練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

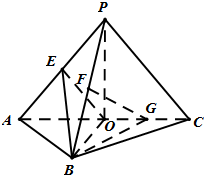如圖，△PAC與△ABC是均以AC為斜邊的等腰直角三角形，AC=4，E，F，O分別為PA，PB，AC的中點，G為OC的中點，且PO⊥平面ABC．
（1）證明：FE∥平面BOG；
（2）求二面角EO-B-FG的余弦值．

查看答案和解析>>

科目：高中數學 來源： 題型：

[選做題]
A．（選修4-1：幾何證明選講）
如圖，△ABC是⊙O的內接三角形，PA是⊙O的切線，PB交AC于點E，交⊙O于點D，若PE=PA，
∠ABC=60°，PD=1，BD=8，求BC的長．
B．（選修4-2：矩陣與變換）
二階矩陣M對應的變換將點（1，-1）與（-2，1）分別變換成點（-1，-1）與（0，-2）．
（Ⅰ）求矩陣M的逆矩陣M-1；
（Ⅱ）設直線l在變換M作用下得到了直線m：2x-y=4，求l的方程．
C．（選修4-4：坐標系與參數方程）
在極坐標系中，設圓ρ=3上的點到直線ρ(cosθ+
3
sinθ)=2的距離為d，求d的最大值．
D．（選修4-5：不等式選講）
設a，b，c為正數且a+b+c=1，求證：(a+
1
a
)2+(b+
1
b
)2+(c+
1
c
)2≥
100
3
．

查看答案和解析>>

科目：高中數學 來源： 題型：

如圖，△ABC和△A1AC是正三角形，平面A1AC⊥底面ABC，A1B1⊥∥AB，A1B1=AB=2，
（I）求直線AA1與平面AB1C所成角的正弦值大小；
（II）已知點D是A1B1的中點，在平面ABCD內擱一點E，使DE⊥平面AB1C，求點E到AC和B的距離．

查看答案和解析>>

科目：高中數學 來源： 題型：

(1)在△ABC中,D是上一點,=,設=a,=b,試用a、b表示.

(2)設DEF三等分△ABC所在各邊，即BC=3BD,CA=3CE,AB=3AF(如圖).

求證:△ABC與△DEF有相同的重心.

查看答案和解析>>

科目：高中數學 來源： 題型：

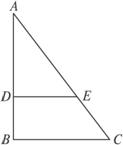
如圖,在△ABC中,B=90°,AC=,D、E兩點分別在AB、AC上,使=2,DE=3.現將△ABC沿DE折成直二面角,求:

(1)異面直線AD與BC的距離;

(2)二面角A-EC-B的大小(用反三角函數表示).

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 久久免费精品视频 | 国产一级在线观看 | 四虎永久免费在线 | 九九精品视频在线观看 | 欧美天天 | 中文字幕av免费 | 免费日本视频 | 国产精品s色 | 狠狠狠干 | 农村少妇kkkk7777 | 六月丁香在线观看 | 草久在线视频 | 久久国产视频一区二区 | 日本一区二区三区精品视频 | 日本高清久久 | 日本成人一区二区 | 久久国产美女 | 成人精品视频 | 日韩欧美国产一区二区三区 | 欧美日韩一区二区不卡 | 欧美一区二区三区成人 | 国产精品亚洲视频 | jizz国产免费 | 亚洲免费av在线 | 国产区免费观看 | 中文字幕精品一区二区三区精品 | 2024男人天堂| 精品国产一区二区三区在线观看 | 亚州中文 | 久久九九国产精品 | 国产麻豆乱码精品一区二区三区 | 国产美女视频黄a视频免费 国产美女在线播放 | 中文字幕免费看 | 日本色一区 | 国产精品自拍一区 | 999精品一区 | 国模一区二区三区 | 黄色电影在线免费观看 | 欧美视频免费在线观看 | 国产精品嫩草99av在线 | 不卡久久|