
【題目】已知函數![]()
(1)當x∈[0,π]時,f(x)≥0恒成立,求實數a的取值范圍;(參考數據:sin1≈0.84)
(2)當a=1時,數列{an}滿足:0<an<1,![]() =f(an),求證:{an}是遞減數列.
=f(an),求證:{an}是遞減數列.
【答案】(1)![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】
求導![]() ,
,![]() ,分
,分![]() ,
,![]() ,
, ![]() 三種情況討論求解.
三種情況討論求解.
(2)要證{an}是遞減數列.即證![]() ,由a=1,構造函數
,由a=1,構造函數![]() ,用導數法證明
,用導數法證明![]() 即可.
即可.
因為![]() ,所以
,所以![]() ,
,
設![]() ,
,
當![]() 時,即
時,即![]() 時,因為
時,因為![]() ,
,
所以![]() ,而
,而![]() ,所以
,所以![]()
即f(x)≥0恒成立,
當![]() 時,
時,![]() ,
,
所以![]() 在[0,π]上遞增,而
在[0,π]上遞增,而![]() ,
,
所以![]() ,所以
,所以![]() 在[0,π]上遞增,
在[0,π]上遞增,
即![]() 成立,
成立,
當![]() 時,
時,![]() ,
,
所以![]() 在[0,π]上遞增,
在[0,π]上遞增,
而![]() ,
,
所以存在![]() ,有
,有![]() ,
,
當![]() 時,
時,![]() ,
,![]() 遞減,
遞減,
當![]() 時,
時,![]() ,
,![]() 遞增,
遞增,
所以當![]() 時,
時,![]() 取得最小值,最小值為
取得最小值,最小值為![]() ,
,
而![]() ,不成立
,不成立
綜上:實數a的取值范圍![]() .
.
(2)因為a=1,所以![]() ,
,
令![]() ,
,
所以![]() ,設
,設![]()
所以![]() ,
,
所以![]() 在
在![]() 上遞增,
上遞增,
而![]() ,
,
所以存在![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,
,![]() 遞減,
遞減,
當![]() 時,
時,![]() ,
,![]() 遞增,
遞增,
而![]() ,
,
所以![]() ,
,
即當![]() 時,
時,![]() ,
,
而![]() ,
,![]() ,
,
所以{an}是遞減數列.


科目:高中數學 來源: 題型:
【題目】設數列![]() 的前n項和為
的前n項和為![]() ,
,![]()
(1)求證:數列![]() 是等比數列;
是等比數列;
(2)若![]() ,是否存在q的某些取值,使數列
,是否存在q的某些取值,使數列![]() 中某一項能表示為另外三項之和?若能求出q的全部取值集合,若不能說明理由.
中某一項能表示為另外三項之和?若能求出q的全部取值集合,若不能說明理由.
(3)若![]() ,是否存在
,是否存在![]() ,使數列
,使數列![]() 中,某一項可以表示為另外三項之和?若存在指出q的一個取值,若不存在,說明理由.
中,某一項可以表示為另外三項之和?若存在指出q的一個取值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的非負半軸為極軸且取相同的單位長度建立極坐標系,曲線
軸的非負半軸為極軸且取相同的單位長度建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的參數方程;
的參數方程;
(2)若![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ),將
),將![]() 的圖象上所有點的橫坐標縮短到原來的
的圖象上所有點的橫坐標縮短到原來的![]() 倍(縱坐標不變),再將得到的圖象上所有點向右平行移動
倍(縱坐標不變),再將得到的圖象上所有點向右平行移動![]() 個單位長度,得到
個單位長度,得到![]() 的圖象,則以下關于函數
的圖象,則以下關于函數![]() 的結論正確的是( )
的結論正確的是( )
A.若![]() ,
,![]() 是
是![]() 的零點,則
的零點,則![]() 是
是![]() 的整數倍
的整數倍
B.函數![]() 在區間
在區間![]() 上單調遞增
上單調遞增
C.點![]() 是函數
是函數![]() 圖象的對稱中心
圖象的對稱中心
D.![]() 是函數
是函數![]() 圖象的對稱軸
圖象的對稱軸
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某保險公司為客戶定制了5個險種:甲,一年期短險;乙,兩全保險;丙,理財類保險;丁,定期壽險:戊,重大疾病保險,各種保險按相關約定進行參保與理賠.該保險公司對5個險種參保客戶進行抽樣調查,得出如下的統計圖例,以下四個選項錯誤的是( )



A.54周歲以上參保人數最少B.18~29周歲人群參保總費用最少
C.丁險種更受參保人青睞D.30周歲以上的人群約占參保人群的80%
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】CPI是居民消費價格指數(comsummer priceindex)的簡稱.居民消費價格指數是一個反映居民家庭一般所購買的消費品價格水平變動情況的宏觀經濟指標.如圖是根據國家統計局發布的2019年4月——2020年4月我國CPI漲跌幅數據繪制的折線圖(注:2019年6月與2018年6月相比較,叫同比;2019年6月與2019年5月相比較,叫環比),根據該折線圖,則下列結論正確的是( )
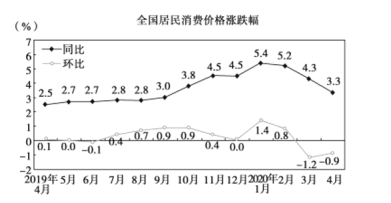
A.2019年4月至2020年4月各月與去年同期比較,CPI有漲有跌
B.2019年4月居民消費價格同比漲幅最小,2020年1月同比漲幅最大
C.2020年1月至2020年4月CPI只跌不漲
D.2019年4月至2019年6月CPI漲跌波動不大,變化比較平穩
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).設
為參數).設![]() 與
與![]() 的交點為
的交點為![]() ,當
,當![]() 變化時,
變化時,![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求![]() 的普通方程;
的普通方程;
(2)設![]() 為圓
為圓![]() 上任意一點,求
上任意一點,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com