
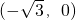 和F2
和F2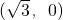 是橢圓M:
是橢圓M: 的兩個焦點,且橢圓M經過點
的兩個焦點,且橢圓M經過點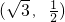 .
.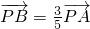 ,求直線l的方程;
,求直線l的方程; ,設橢圓的方程
,設橢圓的方程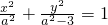 ,
,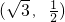 代入得
代入得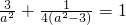 ,解得a2=4,
,解得a2=4, .
.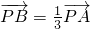 不適合條件;
不適合條件;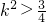 .
. .
.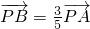 ,即
,即 ,所以
,所以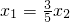 .
.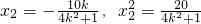 ,解得k=±1,
,解得k=±1, ,并整理得:(1+4k2)x2+16kx+12=0,
,并整理得:(1+4k2)x2+16kx+12=0,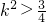 .
. .
.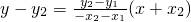 ,
,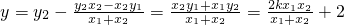 .
. 代入上式得:
代入上式得: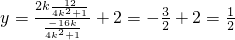 .
. .
.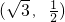 滿足橢圓的方程即可得出.
滿足橢圓的方程即可得出.

科目:高中數學 來源:海淀區二模 題型:單選題
| PF1 |
| PF2 |
| A.0 | B.1 | C.2 | D.2
|
查看答案和解析>>
科目:高中數學 來源:2013年山東省濟南市高考數學二模試卷(文科)(解析版) 題型:解答題
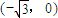 和F2
和F2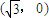 是橢圓M:
是橢圓M: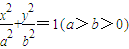 的兩個焦點,且橢圓M經過點
的兩個焦點,且橢圓M經過點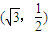 .
.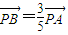 ,求直線l的方程;
,求直線l的方程;查看答案和解析>>
科目:高中數學 來源:2010年上海市寶山區高考數學一模試卷(文理合卷)(解析版) 題型:解答題
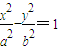 的左右焦點,其漸近線為
的左右焦點,其漸近線為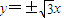 ,且右頂點到左焦點的距離為3.
,且右頂點到左焦點的距離為3.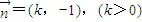 ,且
,且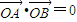 ,求k的值;
,求k的值;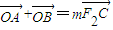 ,求m的值及△ABC的面積S△ABC.
,求m的值及△ABC的面積S△ABC.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com