分析:(Ⅰ)由已知等式,寫出
a1=(21-21+1)b,
a1+2a2=(2•22-22+1)b,由此可求a
1,a
2的值;
(Ⅱ)由已知等式,再寫一式,兩式相減,即可證明數列{2
an}為等比數列;
(Ⅲ)不等式
+++…+>化簡為
(1-)>,分類討論,結合函數的單調性,即可求b和c的取值范圍.
解答:(Ⅰ)解:因為
a1+2a2+22a3+…+2n-1an=(n•2n-2n+1)b,
所以
a1=(21-21+1)b,
a1+2a2=(2•22-22+1)b,
解得a
1=b,a
2=2b.…(3分)
(Ⅱ)證明:當n≥2時,由
a1+2a2+22a3+…+2n-1an=(n•2n-2n+1)b,①
得
a1+2a2+22a3+…+2n-2an-1=[(n-1)•2n-1-2n-1+1]b,②
將①,②兩式相減,得
2n-1an=(n•2n-2n+1)b-[(n-1)•2n-1-2n-1+1]b,
化簡,得a
n=nb,其中n≥2.…(5分)
因為a
1=b,所以a
n=nb,其中n∈N
*.…(6分)
因為
=2an-an-1=2b(n≥2)為常數,
所以數列
{2an}為等比數列.…(8分)
(Ⅲ)解:由(Ⅱ),得
a2n=2nb,…(9分)
所以
+++…+=++…+=×=(1-),…(11分)
又因為
=,
所以不等式
+++…+>化簡為
(1-)>,
當b>0時,考察不等式
(1-)>的解,
由題意,知不等式
1->c的解集為{n|n≥3,n∈N
*},
因為函數
y=1-()x在R上單調遞增,所以只要求
1->c且
1-≤c即可,
解得
≤c<; …(13分)
當b<0時,考察不等式
(1-)>的解,
由題意,要求不等式
1-<c的解集為{n|n≥3,n∈N
*},
因為
1-<1-,
所以如果n=3時不等式成立,那么n=2時不等式也成立,
這與題意不符,舍去.
所以b>0,
≤c<.…(14分)
點評:本題考查數列與不等式的綜合,考查等比數列的證明,考查分類討論的數學思想,考查學生分析解決問題的能力,屬于中檔題.



 ,都有
,都有 (k為常數),則稱{an}為“等差比數列”. 下面對“等差比數列”的判斷: ①k不可能為0;②等差數列一定是等差比數列;③等比數列一定是等差比數列;④通項公式為
(k為常數),則稱{an}為“等差比數列”. 下面對“等差比數列”的判斷: ①k不可能為0;②等差數列一定是等差比數列;③等比數列一定是等差比數列;④通項公式為 的數列一定是等差比數列,其中正確的判斷為( )
的數列一定是等差比數列,其中正確的判斷為( )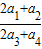 = .
= .