
【題目】已知點A(﹣4,4)、B(4,4),直線AM與BM相交于點M,且直線AM的斜率與直線BM的斜率之差為﹣2,點M的軌跡為曲線C.
(1)求曲線C 的軌跡方程;
(2)Q為直線y=﹣1上的動點,過Q做曲線C的切線,切點分別為D、E,求△QDE的面積S的最小值.
【答案】(1)![]()
![]() (2)最小值4
(2)最小值4
【解析】試題分析:(Ⅰ)設![]() ,由題意得
,由題意得![]() ,化簡可得曲線
,化簡可得曲線![]() 的方程為
的方程為![]()
![]() ; (Ⅱ)設
; (Ⅱ)設![]() ,切線方程為
,切線方程為![]() ,與拋物線方程聯立互為
,與拋物線方程聯立互為![]() ,由于直線與拋物線相切可得
,由于直線與拋物線相切可得![]() ,解得
,解得![]() ,可切點
,可切點![]() ,由
,由![]() ,利用韋達定理,得到
,利用韋達定理,得到![]() ,得到
,得到![]() 為直角三角形,得出三角形面積的表達式,即可求解三角形的最小值.
為直角三角形,得出三角形面積的表達式,即可求解三角形的最小值.
試題解析:(Ⅰ)設M(x,y),由題意可得: ![]() ,
,
化為x2=4y.
∴曲線C 的軌跡方程為x2=4y且(x≠±4).
聯立![]() ,化為x2﹣4kx+4(km+1)=0,
,化為x2﹣4kx+4(km+1)=0,
由于直線與拋物線相切可得△=0,即k2﹣km﹣1=0.
∴x2﹣4kx+4k2=0,解得x=2k.可得切點(2k,k2),
由k2﹣km﹣1=0.∴k1+k2=m,k1k2=﹣1.
∴切線QD⊥QE.
∴△QDE為直角三角形, ![]() |QD||QE|.
|QD||QE|.
令切點(2k,k2)到Q的距離為d,
則d2=(2k﹣m)2+(k2+1)2=4(k2﹣km)+m2+(km+2)2=4(k2﹣km)+m2+k2m2+4km+4=(4+m2)(k2+1),
∴|QD|=![]() ,
,
|QE|=![]() ,
,
∴![]() (4+m2)
(4+m2)![]() =
=![]() ≥4,
≥4,
當m=0時,即Q(0,﹣1)時,△QDE的面積S取得最小值4.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知復數z1=(1+bi)(2+i),z2=3+(1﹣a)i(a,b∈R,i為虛數單位).
(1)若z1=z2 , 求實數a,b的值;
(2)若b=1,a=0,求| ![]() |.
|.
查看答案和解析>>
科目:高中數學 來源: 題型:
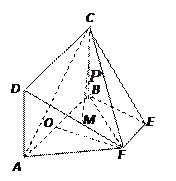
【題目】如圖,矩形ABCD所在的平面和平面![]() 互相垂直,等腰梯形
互相垂直,等腰梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 的中點,
的中點, ![]() 為底面
為底面![]() 的重心.
的重心.
(Ⅰ)求證: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+bx+1(x∈R),(a,b為實數).
(1)若f(1)=0,且函數f(x)的值域為[0,+∞),求f(x)的表達式;
(2)在(1)的條件下,若關于x方程|f(x+1)﹣1|=m|x﹣1|只有一個實數解,求實數m的取值范圍;
(3)在(1)的條件下,求函數h(x)=2f(x+1)+x|x﹣m|+2m最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】解答
(1)求證:函數y=x+ ![]() 有如下性質:如果常數a>0,那么該函數在(0,
有如下性質:如果常數a>0,那么該函數在(0, ![]() ]上是減函數,在[
]上是減函數,在[ ![]() ,+∞)上是增函數.
,+∞)上是增函數.
(2)若f(x)= ![]() ,x∈[0,1],利用上述性質,求函數f(x)的值域;
,x∈[0,1],利用上述性質,求函數f(x)的值域;
(3)對于(2)中的函數f(x)和函數g(x)=﹣x﹣2a,若對任意x1∈[0,1],總存在x2∈[0,1],使得g(x2)=f(x1),求實數a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】集合A={x|(x﹣3)(x﹣a)=0,a∈R},B={x|(x﹣4)(x﹣1)=0},則集合A∪B,A∩B中元素的個數不可能是( )
A.4和1
B.4和0
C.3和1
D.3和0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com